Just a piece of cake

Algebra Level 5

You are running a bakery business with 2 popular strawberry cheesecake products: A & B. Each "cheesy" cheesecake A contains 5 cheese slices in its ingredients while each cheesecake B only needs 3 cheese slices. On the other hand, each "very-strawberry" cheesecake B has 10 strawberries while each cheesecake A has only 5 strawberries. Everyday, there are 240 cheese slices and 300 strawberries available for baking in your stock.

The amount of each kind of cheesecake baked is not fixed, but the total number of cheesecakes must not exceed 50 in one day. (One kind may be baked while the other may not be baked at all.)

If you can profit 2 dollars from each cheesecake A and 3 dollars from each cheesecake B, what is the maximum profit you can earn from selling these cakes in one day? (Assume they are always sold out as they are so yummy!)

The answer is 110.

1 solution

Worranat Pakornrat
Nov 24, 2015

Let x = amount of cheese A baked and y = amount of cheesecake B baked. Now we can set the limiting inequalities as:

5x + 10y ≤ 300; x + 2y ≤ 60 (We can't bake more cheesecakes due to limited strawberry amount.)

5x + 3y ≤ 240 (the cheese slice limit)

x + y ≤ 50 (total amount limit)

x ≥ 0; y ≥ 0

Then we can construct a region bounded by these linear equations: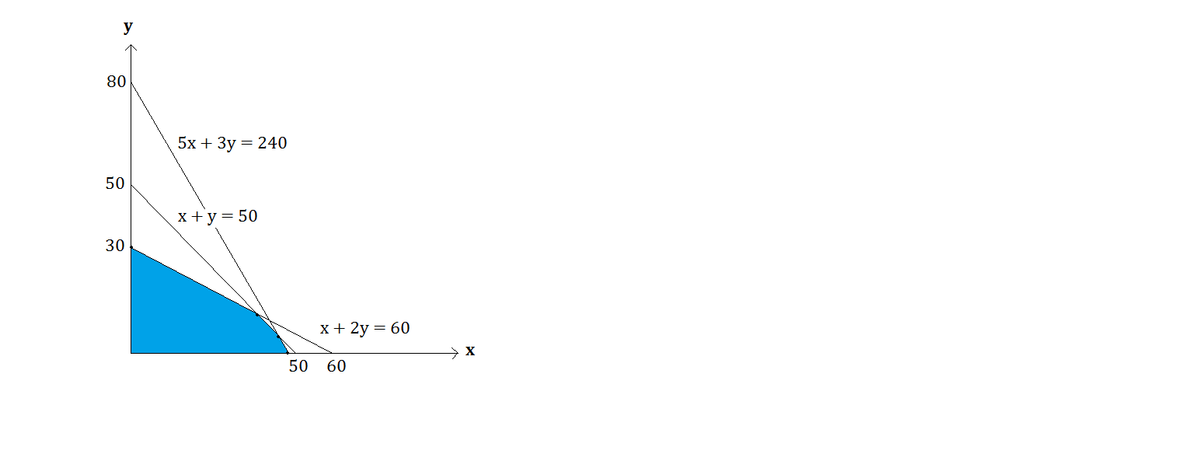

The optimal solution for the maximum profit P = 2x + 3y lies among the vertices of the colored region, which are also the intersections of different linear equations, so there are 5 coordinates to consider: (0 , 0), (0 , 30), (40 , 10), (45 , 5), & (48, 0).

Plugging in these pairs of (x , y), we can calculate for P:

$P(0 , 0) = 0$ $P(0 , 30) = (3\times 30) = 90$ $P(40 , 10) = (40 \times 2) + (10\times 3) = 110$ $P(45 , 5) = (45 \times 2) + (5\times 3) = 105$ $P(48 , 0) = (48 \times 2) = 96$

As a result, to maximize the profit, we should bake 40 cheesecakes A and 10 cheesecakes B, yielding the profit of 110 dollars per day.

Just a piece of cake

The answer is 110.

1 solution

0 pending reports