Just A Quadrant!

The area of the grey region will be the area of the radius $R$ quadrant, namely $\frac{\pi R^{2}}{4}$ , minus the combined areas of the left semicircle, lower semicircle and small circle.

The left semicircle has radius $\frac{R}{2}$ and thus area $(\frac{1}{2})\pi(\frac{R}{2})^{2} = \frac{\pi R^{2}}{8}$ .

To find the area of the lower semicircle, form a right triangle using the centers of the radius $R$ circle, the left semicircle and lower semicircle as vertices. Letting the radius of the lower semicircle be $r$ , the lengths of the two short sides are $\frac{R}{2}$ and $R - r$ , and the hypotenuse has length $\frac{R}{2} + r$ . Then by Pythagoras we have that

$(\frac{R}{2} + r)^{2} = (\frac{R}{2})^{2} + (R - r)^{2}$

$\Longrightarrow \frac{R^{2}}{4} + Rr + r^{2} = \frac{R^{2}}{4} + R^{2} - 2Rr + r^{2} \Longrightarrow 3Rr = R^{2} \Longrightarrow r = \frac{R}{3}$ .

Thus the lower semicircle has area $(\frac{1}{2})\pi(\frac{R}{3})^{2} = \frac{\pi R^{2}}{18}$ .

For the small circle, I will make the assumption that its center lies at $(\frac{2R}{3}, \frac{R}{2})$ , with the origin lying at the center of the radius $R$ circle. This implies that its radius is $\frac{R}{6}$ in order for it to lie horizontally tangent to the left semicircle and vertically tangent to the lower semicircle. To confirm this assumption, we will need to check that the centers of the radius $R$ circle and the small circle are a distance $\frac{5R}{6}$ apart to ensure that these two circles are also tangent to one another. This is the case, since

$\sqrt{(\frac{2R}{3})^{2} + (\frac{R}{2})^{2}} = \sqrt{\frac{4R^{2}}{9} + \frac{R^{2}}{4}} = R\sqrt{\frac{25}{36}} = \frac{5R}{6}$ .

(Note: I'm not entirely happy with this 'guess and confirm' approach to finding the radius of the small circle. If anyone has a better method then please share. :) )

Thus the area of the smaller circle is $\pi(\frac{R}{6})^{2} = \frac{\pi R^{2}}{36}$ .

The area of the grey region is then $\pi R^{2}(\frac{1}{4} - \frac{1}{8} - \frac{1}{18} - \frac{1}{36}) = \frac{\pi R^{2}}{24}$ , and so $X = \boxed{24}$ .

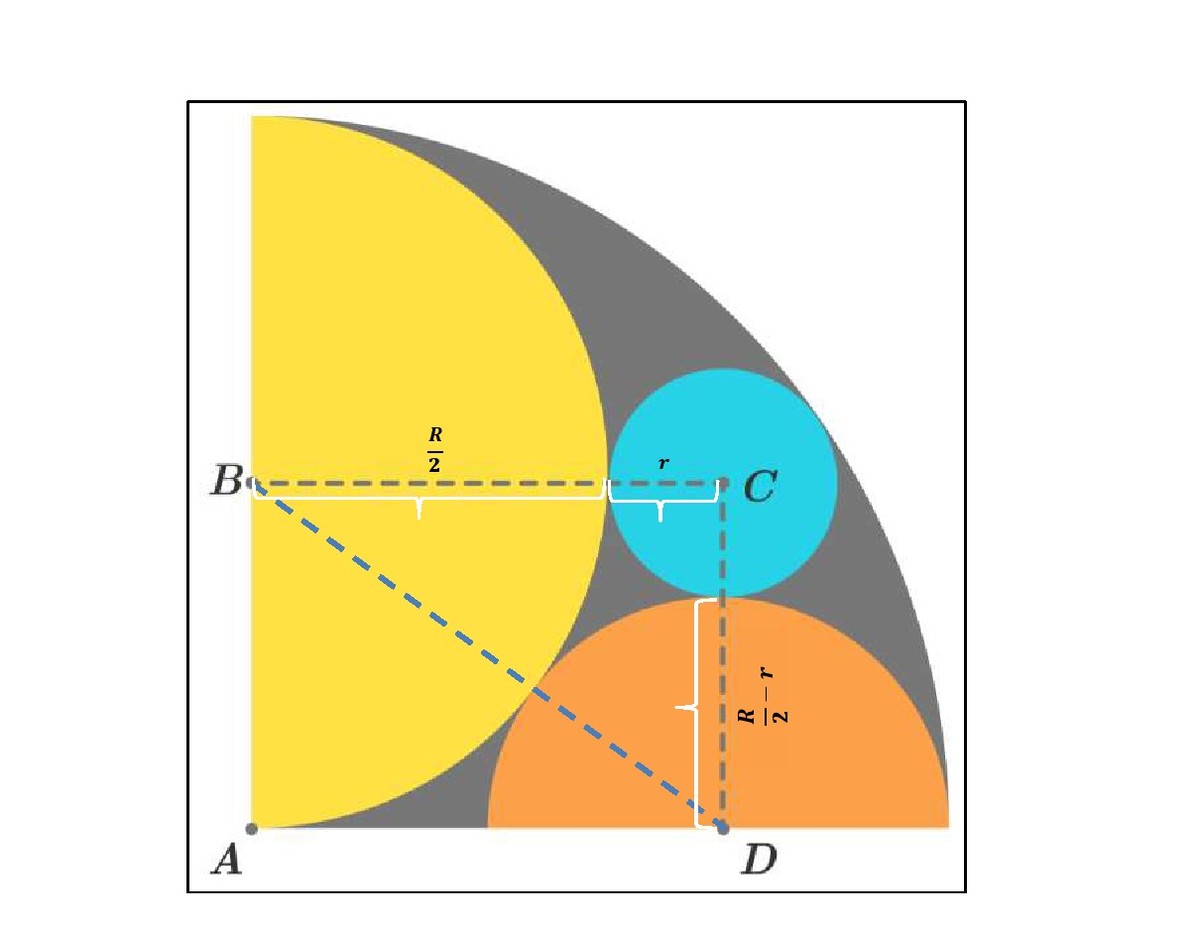
Since $ABCD$ is a rectangle, $BCD$ is a right triangle with $BD$ as the hypotenuse. The yellow semi-circle has radius $\frac{R}{2}$ . Let the radius of the blue circle is $r$ , then the orange semi-circle has radius $\frac{R}{2}-r$ . Now, by Pythagoras we have that

$\begin{aligned}\left(R-r\right)^{2}&=\left(\frac{R}{2}\right)^2+\left(\frac{R}{2}+r\right)^2\\R^2-2Rr+r^2&=\frac{R^2}{2}+Rr+r^2\\r&=\frac{R}{6}\end{aligned}$ .

Now,

$\begin{aligned}A_{1}&=\text{the area of quarter-circle}=\frac{\pi R^2}{4}\\ A_{2}&=\text{the area of the yellow semi-circle}=\frac{\pi R^2}{8}\\ A_{3}&=\text{the area of blue-circle}=\frac{\pi R^2}{36}\\ A_{4}&=\text{the area of the orange semi-circle}=\frac{\pi R^2}{18}\\ A_{5}&=\text{the area of the grey colored region}\\ &=\pi R^2\left(\frac{1}{4}-\frac{1}{8}-\frac{1}{36}-\frac{1}{18}\right)\\ &=\frac{\pi R^2}{24}=\frac{\pi R^2}{X}\end{aligned}$

Thus, $X=24$

Radii are R, R/2, R/3 & R/6

Assume the radius of smaller circle to be x and the smaller semi circle to be y now apply pythagoras theorem in rectangle abcd taking its diagonal as hypotenuese you will get an equation in x, y, and R Now make another quation as x+y=R/2 solve both the equation and gain the value of x and y

Now finding the area of all the the shapes inside the quadrant .sum them up and subtract it from the area of quadrant

There is a way using inverse geometry ( https://en.wikipedia.org/wiki/Inversive_geometry ). A is the origin of the inversion, of radius R. The inverse of the big circle is itself. The inverse of the circle with center B is a horizontal rect line on the top of the bir circle. The inverse of the circle with center D is another circle tangent on the right point, and also tangent to the horizontal line compute before. That mean radius R. The inverse of the smaller circle is tangent to the previous ones, that is much easier to calculate. Computing the inverse of some points, we calculate the radius R/2, R/3 and R/6.

The radius of the quadrant = R The radius of the bigger semicircle = R/2 The radius of the small semicircle = R/3 The radius of the small circle = R/6 Then X = 24

Observe that the radius of the yellow semicircle is $\frac{R}{2}\\$ Let the radius of the orange semicircle = A and the radius of the blue circle = B

1) Observe that $A+B=\frac{R}{2} => B = \frac{R}{2}-A\\$ 2) Observe that $(\frac{R}{2}+B)^2 + (A+B)^2 = (\frac{R}{2}+A)^2\\$ Substituting in yields $(\frac{R}{2}+\frac{R}{2}-A)^2 + (A+\frac{R}{2}-A)^2=(\frac{R}{2}+A)^2\\ => (R-A)^2+(\frac{R}{2})^2=(\frac{R}{2}+A)^2\\ => R^2-2RA+A^2+(\frac{R}{2})^2=(\frac{R}{2})^2+RA+A^2\\ => R^2=3RA => R=3A => A=\frac{R}{3}\\$ From earlier, $B=\frac{R}{2}-A => B=\frac{R}{6}\\$

As per Brian's solution, the $Grey Region = \pi R^2(\frac{1}{4}-\frac{1}{8}-\frac{1}{18}-\frac{1}{36})=\frac{\pi R^2}{24}\\ => X = \boxed{24}$

Let the radius of blue circle be c and that of the orange circle be d. Then clearly, c+d=R/2 and AC²=AD²+DC² or (R-c)²=(R-d)²+(c+d)² which two equations give us: R=6c & d=2c. The grey area = π[R²/4 -c²- 2c² - R²/8] = π[R²/8 -3(R/6)²] =π[R²/8 -R²/12] = π*R²/24

Let the radius of the blue circle be $r$ . We know the radius of the yellow semicircle has to be $\frac{R}{2}$ because twice its radius equals the radius of the big quadrant. It then follows that the radius of the orange semicircle has to be $\frac{R}{2}-r$ . Employing Pythagoras' Theorem, we determine the following equation:

$(\frac{R}{2}+r)^2+(\frac{R}{2})^2=(\frac{R}{2}+\frac{R}{2}-r)^2$

$(\frac{R}{2}+r)^2+(\frac{R}{2})^2=(R-r)^2$

$\frac{R^2}{2^2}+2\times\frac{R}{2}\times r+r^2+\frac{R^2}{2^2}=R^2-2Rr+r^2$

$2\times \frac{R^2}{2^2}+2\times\frac{Rr}{2}+r^2=R^2-2Rr+r^2$

Cancelling factors, we have:

$\frac{R^2}{2}+Rr+r^2=R^2-2Rr+r^2$

Next cancelling $r^2$ , we have:

$\frac{R^2}{2}+Rr=R^2-2Rr$

$R(\frac{R}{2}+r)=R(R-2r)$

Then cancelling $R$ (non-zero common factor),

$\frac{R}{2}+r=R-2r$

$r+2r=R-\frac{R}{2}$

$(1+2)r=\frac{2R-R}{2}$

$3r=\frac{R}{2}$

$r=\frac{R}{3\times2}$

$r=\frac{R}{6}$

Thus, the area of the: - yellow semicircle would be $\frac{1}{2}\times \pi\times(\frac{R}{2})^2=\frac{1}{2}\times \pi \times\frac{R^2}{4}=\frac{\pi\times R^2}{2\times 4}=\frac{\pi R^2}{8}$ - blue circle would be $\pi \times (\frac{R}{6})^2=\frac{\pi R^2}{36}$ - orange semicircle would be $\frac{1}{2}\times \pi\times(\frac{R}{3})^2=\frac{1}{2}\times \pi \times\frac{R^2}{9}=\frac{\pi\times R^2}{2\times 9}=\frac{\pi R^2}{18}$

Adding these areas gives us $\frac{\pi R^2}{8}+\frac{\pi R^2}{36}+\frac{\pi R^2}{18}=\frac{(9+2+4)\pi R^2}{72}=\frac{15\pi R^2}{72}=\frac{5\pi R^2}{24}$ .

With the quadrant an area of $\frac{\pi R^2}{4}$ , the grey region has an area of $\frac{\pi R^2}{4}-\frac{5 \pi R^2}{24}=\frac{(6-5) \pi R^2}{24}=\frac{\pi R^2}{24}$ .

$=> X=\boxed{24}$

Area of the quadrant centred at A is 1/4 πR². Area of semicircle centred at B is: 1/2 π(R/2)²= πR²/8. Area of semicircle centred at D is 1/2 π(R/3)²= πR²/18. Radius of circle centred at C is R/2-R/3=R/6. Area of circle centred at C is : π(R/6)²= πR²/36. Therefore the area of the white region=1/4 πR²-πR²/8-πR²/18-πR²/36=πR²/24 i.e. X=24

Area of the quadrant centred at A is 1/4 πR². Area of semicircle centred at B is: 1/2 π(R/2)²= πR²/8. Area of semicircle centred at D is 1/2 π(R/3)²= πR²/18. Radius of circle centred at C is R/2-R/3=R/6. Area of circle centred at C is : π(R/6)²= πR²/36. Therefore the area of the white region=1/4 πR²-πR²/8-πR²/18-πR²/36=πR²/24 i.e. X=24

same as that of brian's