Just a Regular Nonagon
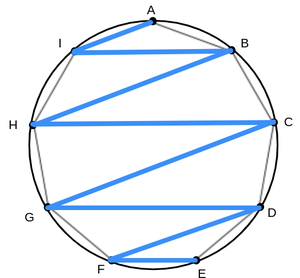
Above, regular nonagon A B C D E F G H I is inscribed in a unit circle. What is the value of the product below?
A I × I B × B H × H C × C G × G D × D F × F E
Hint: Try doing this same method with an inscribed regular triangle and an inscribed square, and see if you see a pattern.
The answer is 9.000.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
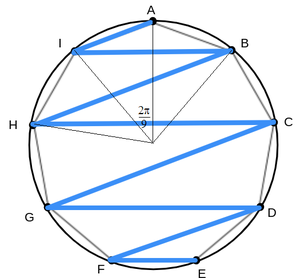
A regular n -sided polygon is made up of n congruent isosceles triangles with its base being the side length of the regular n -gon and central angle of n 2 π . For a regular n -gon inscribed in a unit circle, the length of the two equal sides is 1. Looking at the regular nanogon, we note that A I = 2 sin ( 9 π ) , I B = 2 sin ( 9 2 π ) , B H = 2 sin ( 9 3 π ) , ... F E = 2 sin ( 9 8 π ) . Therefore the product of the lengths is P 9 = 2 sin ( 9 π ) × 2 sin ( 9 2 π ) × 2 sin ( 9 3 π ) × ⋯ × 2 sin ( 9 8 π ) . And for a regular n -gon, we have:
P n = k = 1 ∏ n − 1 2 sin ( n k π ) = 2 n − 1 k = 1 ∏ n − 1 sin ( n k π ) = 2 n − 1 × 2 1 − n n = n See note: k = 1 ∏ n − 1 sin ( n k π ) = 2 1 − n n
Therefore, P 9 = 9 .
Note: See equation 24 .
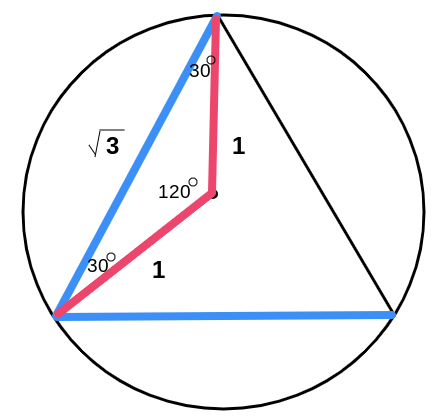
In this inscribed regular triangle, we can find that the length of one of the blue lines is 3 . Because of this, the product of the blue lines is 3 × 3 = 3 . Note that 3 is the total number of sides of the triangle.
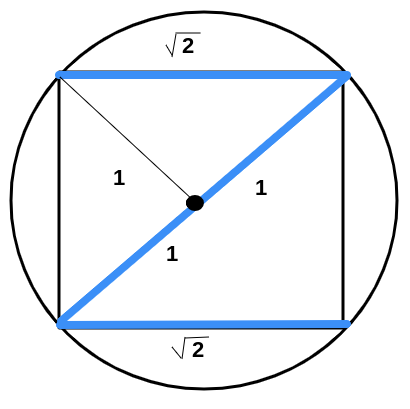
In this inscribed square, we can find that the length of the large line in the middle is two radii or 2 , and that the small lengths are 2 . Because of this, the total product of all blue lines are 2 × 2 × 2 = 4 . Note that 4 is the total number of lengths on the square.
In this inscribed square, we can find that the length of the large line in the middle is two radii or 2 , and that the small lengths are 2 . Because of this, the total product of all blue lines are 2 × 2 × 2 = 4 . Note that 4 is the total number of lengths on the square.
This also holds true on a pentagon, hexagon, septagon/heptagon, and octagon. For proof of this, see the solution by @Joseph Newton . Following this pattern, the product of all the blue lines on the regular nonagon inscribed in a unit circle is 9 , the number of sides on a nonagon.
Here is a general proof for any n -sided polygon the product of the length of the lines is n :
First notice that moving anticlockwise around the circle from A to I we pass no points. Moving clockwise from I to B, we pass one point (A). Moving anticlockwise from B to H we pass two points (A and I). Continuing this pattern, we find that each line passes one more point than the previous one. If we then take every line and move them so that they all start on the same point, we get the following diagram:
This applies to any regular polygon and thus any value of n ≥ 3 .
Now we let the centre of the the circle be the point ( 0 , 0 ) in the complex plane and the point which every line stems from be ( 1 , 0 ) . Since the points are equally spaced on the circle ∣ z ∣ = 1 , they are the n complex solutions to the equation z n − 1 = 0 . Call the non-real solutions z 1 , z 2 , z 3 , … z n − 1 (the n th solution being the real solution z = 1 ). The length of each line now equals the distance from each point to ( 1 , 0 ) , or ∣ 1 − z k ∣ for each k .
Factorising z 9 − 1 = 0 gives ( z − 1 ) ( 1 + z + z 2 + ⋯ + z n − 1 ) = 0 .
However, we can also express the equation in its fully factored form, ( z − 1 ) ( z − z 1 ) ( z − z 2 ) ( z − z 3 ) … ( z − z n − 1 ) = 0 . Therefore, ( z − 1 ) ( z − z 1 ) ( z − z 2 ) ( z − z 3 ) … ( z − z n − 1 ) ( z − z 1 ) ( z − z 2 ) ( z − z 3 ) … ( z − z n − 1 ) Letting ( 1 − z 1 ) ( 1 − z 2 ) ( 1 − z 3 ) … ( 1 − z n − 1 ) = ( z − 1 ) ( 1 + z + z 2 + ⋯ + z n − 1 ) = 1 + z + z 2 + ⋯ + z n − 1 z = 1 : = n 1 ’s 1 + 1 + 1 + ⋯ + 1 = n Now we simply take the absolute value of both sides, and use the identity ∣ x y ∣ = ∣ x ∣ ∣ y ∣ : ∣ ( 1 − z 1 ) ( 1 − z 2 ) ( 1 − z 3 ) … ( 1 − z n − 1 ) ∣ ∣ 1 − z 1 ∣ ∣ 1 − z 2 ∣ ∣ 1 − z 3 ∣ … ∣ 1 − z n − 1 ∣ = ∣ n ∣ = n
Therefore the product of the lengths of the lines is equal to the number of sides of the polygon, so the answer to this question is 9