This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
What do you think @Gabe Smith 's image is doing there / how does it relate to your solution?
Log in to reply
Let's see...
Let S = 1 + 4 3 + 1 6 9 + 6 4 2 7 + …
The first two triangles are similar triangles, therefore the ratio of their sides are the same
1 1 + 4 3 + 1 6 9 + 6 4 2 7 + … = 4 3 4 3 + 1 6 9 + 6 4 2 7 + … 4 3 ( 1 + 4 3 + 1 6 9 + 6 4 2 7 + … ) = 4 3 + 1 6 9 + 6 4 2 7 + … 4 3 S = − 1 + 1 + 4 3 + 1 6 9 + 6 4 2 7 + … 4 3 S = − 1 + S S − 4 3 S = 1 S = 1 − 4 3 1 = 4
We will get the same solution by equating the ratios of the sides of the two triangles
This problem can be seen as a geometric series with a 1 = 1 and common ratio r = 4 3 Thus, the sum is 1 − r a 1 = 1 − 4 3 1 = 4
The diagram helps a lot. Clearly the side length of the bottom length is the sum.
And the slope of the hypotenuse is 4 1 .
So, a glance at the triangle leads us to conclude that the series adds up to 4 .
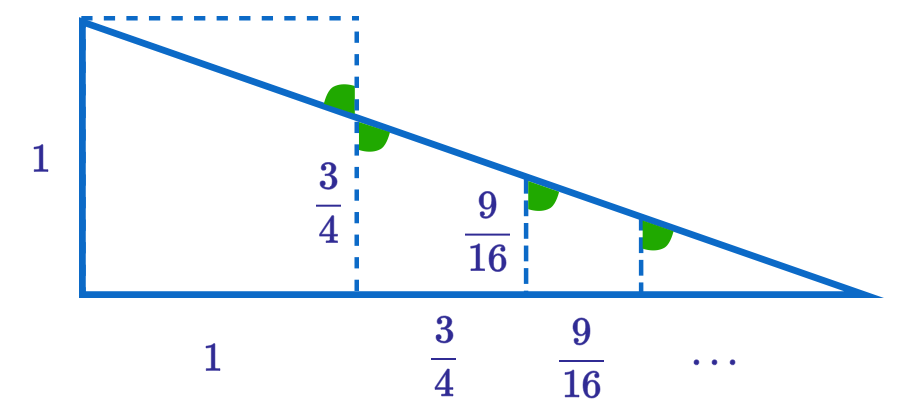

Relevant wiki: Geometric Progression Sum
Notice that 1 + 4 3 + 1 6 9 + 6 4 2 7 + … is a sum of a geometric progression to infinity, where a = 1 and r = 4 3
Therefore, we can use the formula S ∞ = 1 − r a to calculate this
1 + 4 3 + 1 6 9 + 6 4 2 7 + … = 1 − 4 3 1 = 4 1 1 = 4