Just an angle 2
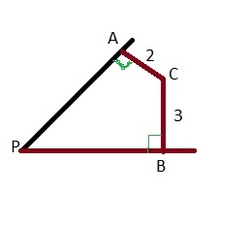 Refer to the above figure. You are given
∠
A
P
B
=
6
0
∘
.
Refer to the above figure. You are given
∠
A
P
B
=
6
0
∘
.
If 3 A P + 2 P B = F E , where E , F are co-prime integers, find E + F .
The answer is 1447.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
Wow .......
I would've loved the trig solution though.
Or should I put it up? Coz I solved using trig
Let P C = x and ∠ A P C = θ , then using sine rule, we have:
sin 9 0 ∘ x = x ⇒ 2 ( sin ( 6 0 ∘ − θ ) ) 2 ( 2 3 cos θ − 2 1 sin θ ) 3 cos θ − sin θ 3 cos θ tan θ A P ∠ C P B tan ( 6 0 ∘ − θ ) P B ⇒ 2 A P + 3 P B ⇒ E + F = sin θ 2 = sin ( 6 0 ∘ − θ ) 3 = 3 sin θ = 3 sin θ = 3 sin θ = 4 sin θ = 4 3 = tan θ 2 = 3 8 = 6 0 ∘ − θ = 1 + 4 3 3 − 4 3 = 7 3 3 = tan ( 6 0 ∘ − θ ) 2 = 3 7 = 3 2 4 + 3 1 4 = 3 3 8 = 3 1 4 4 4 = 1 4 4 7
L e t ∠ C A B = α , ∠ C B A = β , ⟹ S i n P A B = C o s α , S i n P B A = C o s β . In cyclic quadrilateral A P B C , ∠ P = 6 0 , ∴ ∠ C = 1 2 0 Applying Cos Rule to all in Δ A B C , A B 2 = 2 2 + 3 2 − 2 ∗ 2 ∗ 3 ∗ C o s 1 2 0 = 1 9 . C o s α = 2 ∗ 2 ∗ 1 9 2 2 + 1 9 − 3 2 = 2 ∗ 1 9 7 ⟹ S i n P A B = 2 ∗ 1 9 7 . C o s β = 2 ∗ 3 ∗ 1 9 3 2 + 1 9 − 2 2 = 1 9 4 ⟹ S i n P B A = 1 9 4 . S i n 6 0 1 9 = S i n P B A P A = S i n P A B P B ∴ 3 ∗ P A = 3 2 4 , a n d 2 ∗ P B = 3 1 4 ⟹ 3 ∗ P A + 2 ∗ P B = 3 3 8 = 3 3 8 2 . 3 8 2 + 3 = 1 4 4 7
Hint :
→ Produce B C and P A to meet at a point(say D ) and then the question is all yours.
→ Just apply a bit of Trigonometry and Pytagoras Theorem and solve it.
E a s y ! ! , isn't it ?
Firstly drop a perpendicular line from A which intersects PB at u and then draw a line from C that is perpendicular to the line segment AU and intersects AU at V. Now ∠ P A U = 3 0 → ∠ V A C = 6 0 . Also, notice that BCVU is a rectangle as it contains four 90 degree angles. Let AP = x and PB = y then using special triangle (as APU and AVC are both half an equilateral triangle): A U = 2 x 3 = A V + V U = 2 s i n 3 0 + 3 = 1 + 3 = 4 ⇒ x = 3 8 Similarly: P B = P U + U B = P U + V C = 2 x + 2 s i n 6 0 = 3 4 + 3 = 3 7 ⇒ 3 A P + 2 P B = 3 x + 2 y = 3 3 8 = 3 1 4 4 4 ∴ E + F = 1 4 4 7
Note that PACB is cyclic so PA CB+AC PB = PC AB. Using the law of cosines, AB^2 = AC^2+BC^2 - 2AC BC cos(angle ACB). Because PACB is cyclic we know that angle ACB = 180 - angle APB = 120. So AB^2 = 2^2+3^2-2 2 3 (-1/2) = 19. We have that AB = sqrt(19). Since PACB is cyclic, we also know that P is on the circumcircle of ACB which is the circumcircle of PACB. Since P is on the circumcircle of ACB and angle PAC is right, PC is the diameter of the circumcircle of ACB. We know that for a triangle ABC with side lengths a, b, and c we have (AB BC AC)/4[ABC] = R where R is the circumradius of ACB. We know that [ACB] = 1/2 AC BC sin(angle ACB) = 1/2 * 2 3 * sqrt(3) / 2 = (3sqrt(3))/2. So R = (sqrt(19) * 2* 3) / (4 * (3sqrt(3))/2 ) = sqrt(19)/sqrt(3). So PC = 2R = 2sqrt(19)/sqrt(3). Now finally we have that the answer is PC * AB = 2sqrt(19)/sqrt(3) * sqrt(19) = sqrt(1444/3) and thus E+F = 1447.
I used only ptolemy's theorem and sin rule but not trig.
sin rule is trig?
let x = ∣ A P ∣ and y = ∣ P B ∣ :
From pythagorean theorem (forming two triangles △ A P C and △ C P B sharing the same hypotenuse ∣ P C ∣ ):
x 2 + 2 2 = y 2 + 3 2
x 2 − y 2 = 5
Let θ 1 = ∠ A P C and θ 2 = ∠ C P B such that θ 1 + θ 2 = 6 0 ∘ :
2 3 = s i n θ 1 s i n ( 6 0 − θ 1 ) = 2 3 c o t θ 1 − 2 1
Also:
x y = c o s θ 1 c o s ( 6 0 − θ 1 ) = 2 3 t a n θ 1 + 2 1
From these, we can get:
t a n θ 1 = 4 3
and
y = 8 7 x
which yields to
x = 3 8 3
y = 3 7 3
However, we are to solve 3 x + 2 y , which is 3 1 4 4 4 .
I'm usually a fan of trig, but it is absolutely unnecessary here. As in the above picture, extend A C and P B until they meet at Q. Since m ∠ A P B = 6 0 , then m ∠ A Q P = 3 0 and m ∠ Q C B = 6 0 .
You now have two 30-60-90 triangles, which means if you know one side you can know all sides (if you are unfamiliar, the side opposite the 30 = a, the side opposite the 60 = a 3 , the side opposite the 90 = 2a). So:
1) B C = 3 ⇒ C Q = 6 and B Q = 3 3
2) A Q = 8 ⇒ A P = 3 8 and P Q = 3 1 6
3) P B = P Q − B Q = 3 1 6 − 3 3 = 3 7
Finally, 3 A P + 2 P B = 3 3 8 = 3 1 4 4 4 = F E ⇒ E + F = 1 4 4 7 . □
Note: Scout's honor, I did not see the hint from Akshat Sharda when I came up with this :-)