Just An Equation
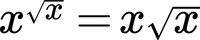
Find the sum of all solutions to the equation above.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Discussions for this problem are now closed
Awesome solution!
Another way I like to think about it/present it is x x = x x = x 2 3 , so either x = 1 or x = 2 3 .
very elegant
x x = x x x ln x = ln ( x x ) x ln x − ln x − ln x 1 / 2 = 0 x ln x − ln x − 2 1 ln x = 0 ( x − 1 − 2 1 ) ln x = 0 Hence, the solutions are: ln x = 0 ⇒ x = 1 or: x − 2 3 = 0 ⇒ x = 9 / 4 1 + 4 9 = 4 1 3
From observation, 1 is a solution, and 0 is not as 0 0 is indeterminate. We also have:
ln ( x x ) = ln ( x x )
x ln x = ln ( x 2 3 ) = 2 3 ln x
x = 2 3
x = 4 9
Therefore the sum of the solutions is 1 + 4 9 = 4 1 3 .
x x = x x e x l n x = e l n ( x x ) x l n x = 2 3 ⋅ l n x → x 1 = 1 x = 2 3 → x 2 = 9 4 x 1 + x 2 = 4 1 3
First note that x = 0 is not a solution, since 0 ∗ 0 = 0 but 0 0 = 0 0 is indeterminate. So given that x = 0 , we can write this equation as
x 2 3 x x = 1 ⟹ x ( x − 2 3 ) = 1 .
Now since 1 y = 1 for any real y we have that x = 1 is a solution.
For x = 1 , 0 we must have that x − 2 3 = 0 ⟹ x = ( 2 3 ) 2 = 4 9 .
The sum of all possible solutions is thus 1 + 4 9 = 4 1 3 .