Just An Inscribed Square

Calculus Level 3

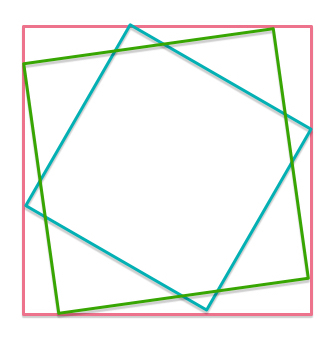
A square $PQRS$ is inscribed inside a square $ABCD$ , with $P$ on $AB$ . If $P$ is uniformly distributed along side $AB$ , the expected area of $PQRS$ is $24\text{ unit}^2$ . What is the side length of square $ABCD$ (in $\text{unit}$ )?

Give your answer to 1 decimal place.

The answer is 6.0.

1 solution

Efren Medallo
Aug 13, 2016

Let $x$ be the nearest distance of one vertex of PQRS to one vertex of ABCD along the larger square. If Square ABCD has side length $s$ , then the area of Square PQRS is given by:

$A(x) = x^2 + (s-x)^2$ $A(x) = 2x^2 - 2sx + s^2$ Note that this was the very method used to prove the Pythagorean Theorem.

Now, to find the average value, we have:

$A(x)_{ave} = \large { \frac{ \int_0^s A(x) dx}{s-0} }$

$A(x)_{ave} = \large { \frac {\int_0^s 2x^2 - 2sx + s^2 dx}{s} }$

$A(x)_{ave} = \frac { \frac{2}{3}x^3 - sx^2 + s^2x |_{0}^{s} }{s}$

$A(x)_{ave} = \frac { \frac{2}{3}s^3 }{s}$

$A(x)_{ave} = \frac{2}{3} s^2$

So now we have found out the average area of PQRS in terms of $s$ .

We can now equate this to 24 to find the value of $s$ .

$\frac{2}{3}s^2 = 24$

$s^2 = 36$

$\boxed {s = 6 }$

The distribution of squares to take the average is extremely important. Is it uniformly distributed by the "vertex along AB", or by the "angle that it makes with respect to AB"? This will yield different integration probabilities.

Calvin Lin Staff - 4 years, 10 months ago

The method I used here, sir, follows the distribution of the former. I will edit the problem accordingly. Thank you!

Efren Medallo - 4 years, 10 months ago

Note: You are not using the mean value theorem . You are simply calculating the expected area of the square.

Calvin Lin Staff - 4 years, 10 months ago

Just An Inscribed Square

The answer is 6.0.

1 solution

0 pending reports