Just Another 3-4-5 Triangle

Geometry Level 5

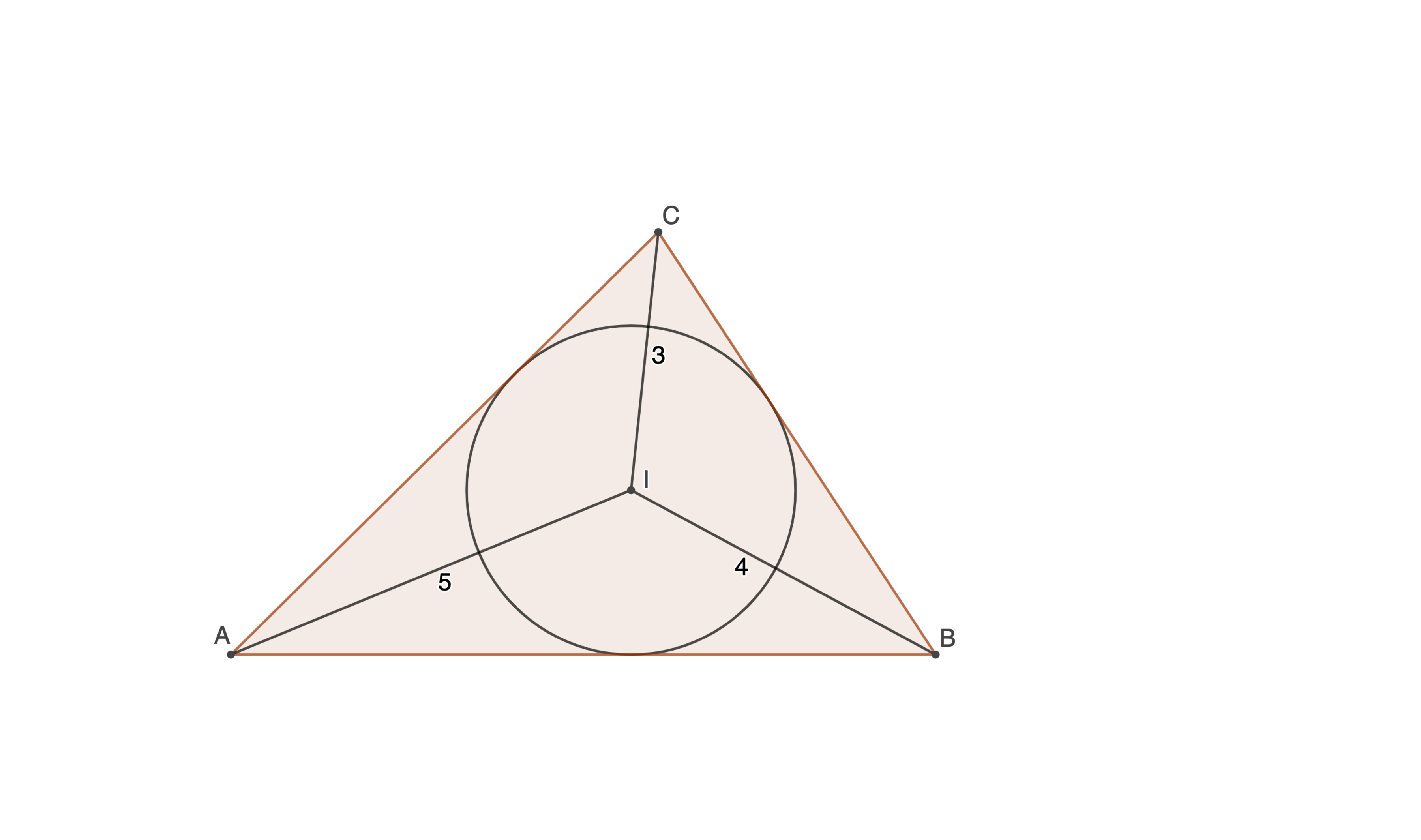
Find the area of the non-degenerate triangle with the distances between its vertices and its incenter, I I , equal to 3, 4, and 5.

If K K is the area, submit ⌊ 1 0 4 K ⌋ \lfloor 10^4K\rfloor .


The answer is 198877.

Fletcher Mattox by Fletcher Mattox , 72, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Chris Lewis
Apr 29, 2021

Let the inradius of Δ A B C \Delta ABC be r r . Recall the incentre I I lies on the three angle bisectors of Δ A B C \Delta ABC be r r . By considering Δ A I C \Delta AIC , we have sin ⁡ C 2 = r 3 \sin\frac{C}{2}=\frac{r}{3}

Now, in Δ A I B \Delta AIB , we have ∠ I A B = A 2 \angle IAB=\frac{A}{2} , ∠ I B A = A 2 \angle IBA=\frac{A}{2} and so ∠ A I B = π − A 2 − B 2 = π − A + B 2 = π − π − C 2 = π 2 + C 2 \angle AIB=\pi-\frac{A}{2}-\frac{B}{2}=\pi-\frac{A+B}{2}=\pi-\frac{\pi-C}{2}=\frac{\pi}{2}+\frac{C}{2}

Also, ∠ A I B = cos ⁡ − 1 r 5 + cos ⁡ − 1 r 4 \angle AIB=\cos^{-1} \frac{r}{5}+\cos^{-1} \frac{r}{4}

Putting these together and taking cosines, cos ⁡ ( cos ⁡ − 1 r 5 + cos ⁡ − 1 r 4 ) = cos ⁡ ( π 2 + C 2 ) r 5 ⋅ r 4 − 1 − r 2 5 2 ⋅ 1 − r 2 4 2 = − sin ⁡ C 2 r 2 20 − ( 1 − r 2 25 ) ( 1 − r 2 16 ) = − r 3 \begin{aligned} \cos \left(\cos^{-1} \frac{r}{5}+\cos^{-1} \frac{r}{4}\right) &= \cos \left(\frac{\pi}{2}+\frac{C}{2}\right) \\ \frac{r}{5} \cdot \frac{r}{4} - \sqrt{1-\frac{r^2}{5^2}} \cdot \sqrt{1-\frac{r^2}{4^2}} &=-\sin \frac{C}{2} \\ \frac{r^2}{20} - \sqrt{\left(1-\frac{r^2}{25}\right)\left(1-\frac{r^2}{16}\right)} &=-\frac{r}{3} \end{aligned}

Rearranging and squaring, r 2 20 + r 3 = ( 1 − r 2 25 ) ( 1 − r 2 16 ) r 4 400 + r 3 30 + r 2 9 = 1 − r 2 25 − r 2 16 + r 4 400 r 3 30 + r 2 9 = 1 − r 2 25 − r 2 16 \begin{aligned} \frac{r^2}{20}+\frac{r}{3} &= \sqrt{\left(1-\frac{r^2}{25}\right)\left(1-\frac{r^2}{16}\right)} \\ \frac{r^4}{400}+\frac{r^3}{30}+\frac{r^2}{9} &=1-\frac{r^2}{25}-\frac{r^2}{16}+\frac{r^4}{400} \\ \frac{r^3}{30}+\frac{r^2}{9} &=1-\frac{r^2}{25}-\frac{r^2}{16} \end{aligned}

which after tidying the fractions becomes 120 r 3 + 769 r 2 − 3600 = 0 120r^3+769r^2-3600=0 This has a unique positive root, around r = 1.9002 r=1.9002 . From here, we can work out the sides using c = A B = 5 2 − r 2 + 4 2 − r 2 c=AB=\sqrt{5^2-r^2}+\sqrt{4^2-r^2} and so on; the area is T = 1 2 r ( a + b + c ) = 19.8877 … T=\frac12 r(a+b+c)=19.8877\ldots giving the answer 198877 \boxed{198877} .

1 Helpful 1 Interesting 3 Brilliant 0 Confused

The way the r 4 r^4 terms cancel is suspiciously neat - it makes me think there's a quicker way to get to the cubic. Also, the cubic itself is a bit surprising - I think it means it wouldn't be possible to construct this with straight-edge and compass.

Oh, and in general, that cubic is 2 r 3 A I ⋅ B I ⋅ C I + r 2 [ 1 A I 2 + 1 B I 2 + 1 C I 2 ] = 1 \frac{2r^3}{AI\cdot BI \cdot CI}+r^2 \left[\frac{1}{AI^2}+\frac{1}{BI^2}+\frac{1}{CI^2}\right]=1

I think this always has a unique positive root, meaning for any A I , B I , C I AI,BI,CI there is a unique triangle, but I haven't looked into it too rigorously (Descartes' rule of signs seems enough, but I could be wrong).

Chris Lewis - 1 month, 2 weeks ago

Log in to reply

Re your last paragraph: Yes Descartes' rule of signs is the key here.

Another great solution by the way.

Pi Han Goh - 1 month, 1 week ago
Saya Suka
Apr 28, 2021

With an inradius x, I used 2 area formulae to get

x² = √[(9 – x²)(16 – x²)(25 – x²)] / [√(9 – x²) + √(16 – x²) + √(25 – x²)]

Then, using the positive real result of x ≈ 1.9002 to get the area of triangle
= x[√(9 – x²) + √(16 – x²) + √(25 – x²)]
= 19.8877955

Answer
= floor[ 10⁴ × 19.8877955 ]
= 198877

1 Helpful 0 Interesting 2 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...