Just around the riverbend
A river winds through the countryside, as shown in the image above. During the melt season, the water level in the river can overflow the banks, ruining the surrounding land. To combat the rise in water level, townspeople band together to build dikes on the shore. This is easy enough to do in the straight sections, as the dike simply has to resist the static pressure of the water. However, we must consider the circular motion of the water at the bends in the river.
Consider a bend in a section of the river such that the outer bank follows a semi-circle of radius . Further suppose that the river is uniformly wide from bank to bank. Finally, the water level rises a height above its usual level, and the water flows uniformly at m/s.
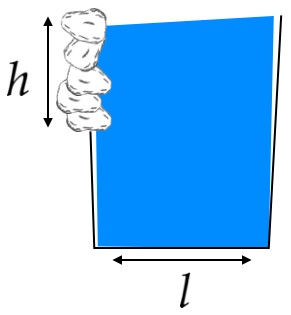
Find the minimum pressure (in Pa = N/m ) the wall must be able to resist.
Assumptions and Details
- Hint: the bottom of the wall must be stronger than the top.
- m, m, m/s, m
- The density of water is kg/m
The answer is 36900.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Pressure due the weight of water equals d g h at the very bottom of the wall, and pressure due to the centrifugal force exerted by water can be calculated as follows:
A small volume of water, of height h , length l and width Δ x , has its centre of mass traveling with speed v along a circle of radius r . (Actually every molecule has the path of radius r ).
So, P = F / A = d h l Δ x v 2 / r / h Δ x = d l v 2 / r The total minimum pressure is then d g h + d l v 2 / r . The wall can be made stronger but it should be able to resist at least 36900 Pa.