Just be quick with calculations
A B C is an equilateral triangle such that vertices B , C lie on two parallel lines at a distance of 6 units. If A lies between the parallel lines at a distance 4 units from one of them, then the length of the side of the triangle is of the form A C B , where A , B , C are co prime natural numbers.
Find A + B + C .
The answer is 14.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
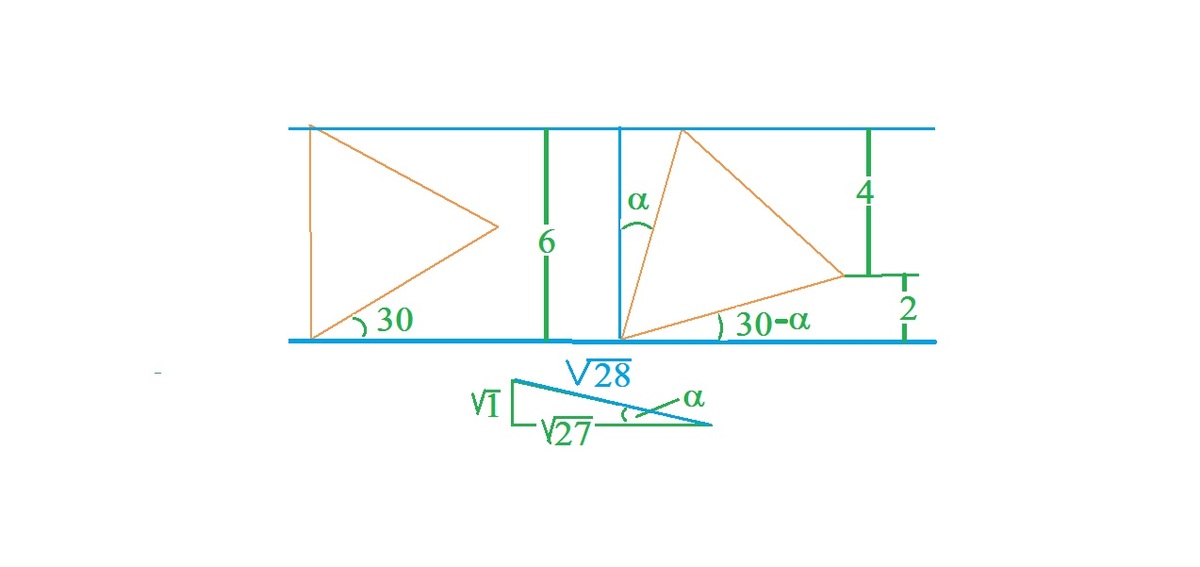Let vertical side be tilted through
∠
α
∴
s
i
d
e
x
=
C
o
s
α
6
a
n
d
x
∗
S
i
n
(
3
0
−
α
)
=
2
.
⟹
S
i
n
(
3
0
−
α
)
=
2
∗
6
C
o
s
α
2
1
∗
C
o
s
α
−
2
3
∗
S
i
n
α
=
3
C
o
s
α
⟹
−
2
3
∗
S
i
n
α
=
−
6
C
o
s
α
⟹
T
a
n
(
α
)
=
3
3
1
S
e
c
(
α
)
=
2
7
2
8
x
=
6
∗
S
e
c
(
α
)
x
=
4
∗
3
7
x
=
A
∗
C
B
A
+
B
+
C
=
1
4
Are u really 87 yrs old!!
Log in to reply
It is OK to question. But wanted to know why did your question? Just wanted to know. Yes I am running 78.
the missing steps are
as θ is acute taking only positive value