Just Differentiate It!

Geometry Level 1

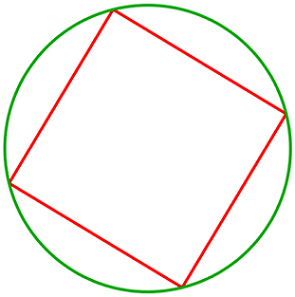
A square is inscribed in a circle . If the area of the circle is π 2 \pi^2 , what is the area of the square?

π \pi 2 π 2\pi 3 π 3\pi 4 π 4\pi

View wiki
Pi Han Goh by Pi Han Goh , 30, Malaysia

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

3 solutions

Since area if circle is π 2 π^2 , radius of the circle is π \sqrt{π} .

Diameter of circle = Diagonal of square = 2 π 2\sqrt{π} .

Therefore side of the square is 2 π 2 = 2 π \dfrac{2\sqrt{π}}{\sqrt2}=\sqrt{2π} .

Therefore area of square is 2 π 2π .

6 Helpful 0 Interesting 0 Brilliant 0 Confused

Moderator note:

The diagonal of the square could be found by applying Pythagorean Theorem ,

( \side length ) 2 + ( \side length ) 2 = ( diagonal of square ) 2 = ( diameter of circle ) 2 . (\text{\side length})^2 + (\text{\side length})^2 = (\text{diagonal of square})^2 = (\text{diameter of circle})^2 .

Since we know that the diameter of the circle is twice its radius, then 2 ( side length ) 2 = ( 2 π ) 2 2(\text{side length})^2 = (2 \sqrt\pi)^2 .

And because we know that the area of a square is simply the square of its side length, then the answer is 1 2 ( 2 π ) 2 = 2 π \dfrac12 (2\sqrt\pi)^2 = 2\pi .

Andrea Gallese
Aug 11, 2016

Just differentiate d π 2 d π = 2 π \frac{d \pi ^2}{d \pi} = 2\pi

3 Helpful 0 Interesting 0 Brilliant 0 Confused

please explain how differentiating gives us answer ??

Chirayu Bhardwaj - 4 years, 10 months ago

Im whith chiravu

Singal Parth - 4 years, 10 months ago

Please explain

Anirudha Brahma - 4 years, 10 months ago
Md Zuhair
Aug 4, 2016

Here we see that A = π 2 A = \pi^2 And we also know that π r 2 = π 2 \pi r^2 = \pi^2 .... Or r = π r = \sqrt{\pi} ... and A 2 = π \frac{A}{\sqrt{2}} = \sqrt{\pi} .. Solving for a 2 a^2 we get 2 π 2\pi

2 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...