Just for fun!

Fact 1: Yes, to select a multiple choice option quickly, try plugging in each of the options. Only $\boxed{x=y=1 \ \text{and} \ x=y=-2}$ works, so that is the answer.

Fact 2: If this were not a multiple choice question, than solving this simple-looking algebra problem would be extremely tricky!

As given, the equations are

$\begin{cases} x^{4}+5y=6 \\ x^{2}.y^{2}+5x=6 \end{cases}$

These are some strange equations, and the method for solving them is also more than a little weird.

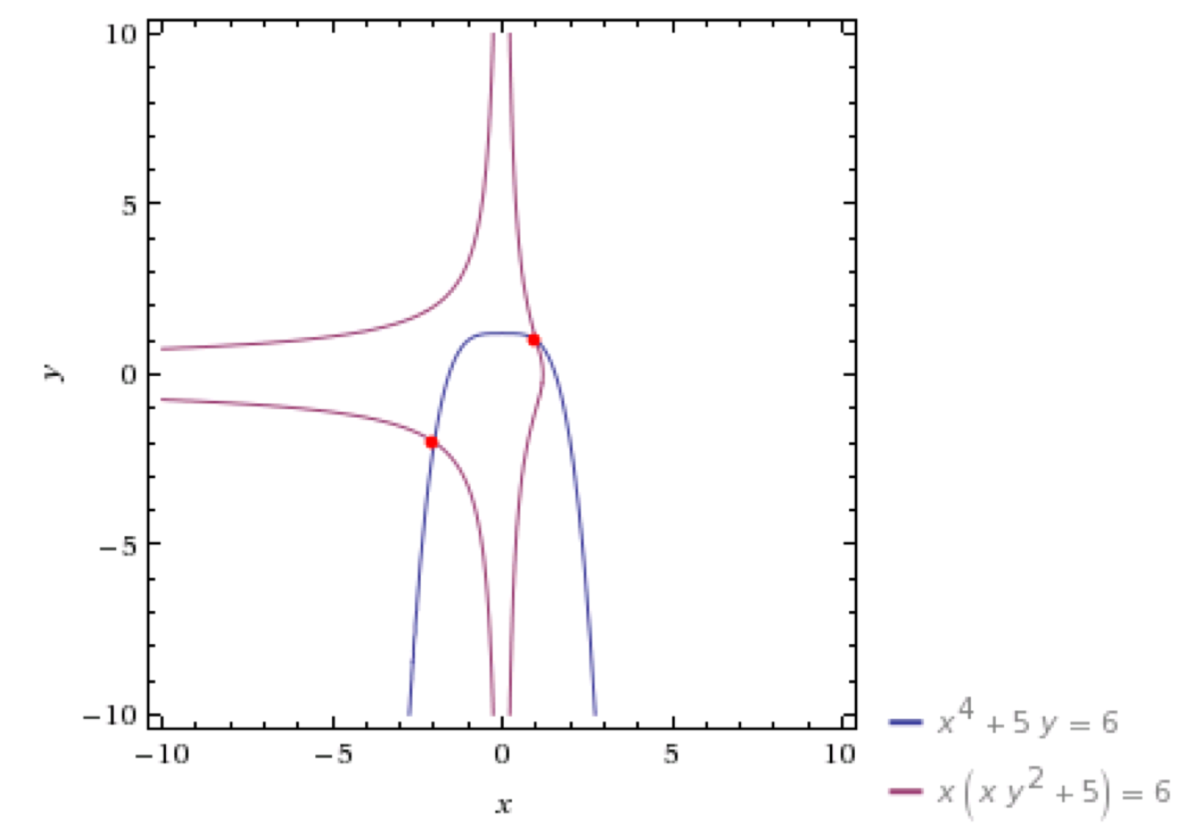
Because the right hand sides of both equation are both $=6$ , we can set the two left-hand sides of the equations as equal to each other as well. Notably, this does lose some information. For example, if we had the equation set $a+b = 1$ and $2b=1$ , that would imply that $a+b=2b\ \Rightarrow a = b$ . So the solutions to this would seem to be all values that satisfy $a=b$ until we go back and reuse at least one of the original equations, say $2b=1$ , to conclude that only the solution $a=b=\frac{1}{2}$ actually satisfies both of the original equations. We'll need to do something very similar here, but we can start with the same approach.

We begin by setting the left-hand-sides of both equations equal to each other:

$\begin{array}{c}& x^{4}+5y=x^{2} y^{2}+5x \\ \Rightarrow & x^{4}-x^{2}y^{2}=5(x-y) \\ \Rightarrow & x^{2}[x^{2}-y^{2}]=5(x-y) \\ \Rightarrow & x^{2}(x+y)(x-y)=5(x-y) \end{array}$

Now we can choose between two options moving forward:

1) We can search for solutions that satisfy $x-y=0$ (or, in other words, $x=y$ ). Any such pairs would satisfy the equation $x^{2}(x+y)(x-y)=5(x-y)$ because both sides would be made equal to 0.
2) We can assume that $x-y\neq0$ , and divide both sides of the equation by $x-y$ .

And very importantly in the pursuit of either of these methods, we'll need to recombine one of the original equations back into the mix, so that the " $=6$ " information is brought back into our process.

(1) is the pathway that ultimately leads to two solutions. I'll leave the details for you to track down, but the process is to replace every x in the original equations with a y (since $x=y$ ) and then solve for values of y. The result will be $y=1$ and $y=-2$ , so the final answers are $\boxed{x=y=1 \ \text{and} \ x=y=-2}$ .

(2) winds up not providing any further solutions. Here's a sketch of why: Recall that in this problem-solving fork, we choose to assume that $x-y\neq0$ , and subsequently divide both sides of the equation by $x-y$ .

$\begin{array}{c}& x^{2}(x-y)(x+y)=5(x-y) \\ \Rightarrow & x^{2}(x+y)=5 \end{array}$

We then add back in the information from the original equations, that $x^4+5y=6$ . Solving this equation for $y$ yields $y= \frac{6-x^4}{5}$ . And we'll then take the right hand side and substitute that in for $y$ in $x^4+5y=6$ . The result after some simplification is: $-x^6 + 5x^3 + 6x^2 = 25$ So any solutions to this equation will be additional answers -- solutions to the original system of equations. However, we are going to be disappointed...

Because the leading term is $-x^6$ , this function will have a maximum value and then both ends will ultimately reach towards negative infinity. The question then is: is the maximum value the function reaches greater than 25, so that there will be solutions to the equation? The answer: no. I figured this out using some calculus to solve for the locations of the local extrema of the function and then checking each. Here's a graph:

Multipliquemos a segunda equação por (- 1). Temos que,

$x^4 - x^2y^2 + 5y - 5x = 0 \\\\ x^2(x^2 - y^2) + 5(y - x) = 0 \\\\ x^2(x + y)(x - y) - 5(x - y) = 0 \\\\ (x - y)[x^2(x + y) - 5] = 0 \\\\ (x - y)(x^3 + x^2y - 5) = 0$

Do primeiro fator, $\boxed{x = y}$ .

Substituindo-o numa das equações iniciais,

$x^4 + 5x - 6 = 0 \\\\ (x - 1)(x + 2)(x^2 - x + 3) = 0$

Com efeito, $\boxed{\boxed{x = y = 1}}$ e $\boxed{\boxed{x = y = - 2}}$ .

Alright, @Sandeep Bhardwaj 's solution is quite right. Now I will explain more. As you can see we get 2 situations here:

• $y=x$ so just subtitute it back and we get the values of $x$ and $y$ easily.

• $y=\frac{5}{x^2}-x$ (with $x \not=0$ ) subtitute back in the first equation and we get:

$x^6-5x^3-6x^2+25=0$

From the second equation we have:

$5x=6-x^2y^2 \leq 6 \Rightarrow x \leq \frac{6}{5}$

So we can say that:

$5x^3+6x^2 \leq 5 (\frac{6}{5})^3+6 (\frac{6}{5})^2 <25$

That means:

$x^6-5x^3-6x^2+25>0$

So there is no solution for this situation.

check the options given ( far more easy way than @Sandeep Bhardwaj )!! bt still its gud!!

$x^4 + 5y = x^{2}y^{2} + 5x = 6$

$x^2(x + y)(x - y) - 5(x - y) = 0 \Rightarrow \begin{cases}{x = y}\\{x^{2}(x + y) = 5}\end{cases}$

$x = y \Rightarrow x^4 + 5x - 6 = 0 \Rightarrow (x - 1)(x + 2)(x^2 - x + 3) = 0 \Rightarrow \boxed{x = y = 1 , -2}$

$x^{2}y^{2} + 5x = 6 \Rightarrow x < \dfrac{6}{5}$

$x^4 + 5y + x^{2}y^{2} + 5x = 12 \Rightarrow x + y < \dfrac{12}{5}$

$\Rightarrow x^{2}y^{2}(x + y) < (\dfrac{6}{5})^{2}\times{\dfrac{12}{5}} < 5 \Rightarrow \text{no solutions}$

$\therefore \boxed{(x , y) = (1 , 1) , (-2 , -2)}$

Since it is multiple choice, just check the given options to find the answer x=y=-2 or x=y=1

It is easy to see x=y=1 is an obvious solution. So the only multiple choice option that has this is : x=y=-2 or x=y=1. So we are done.

All I did was just try out each solution given in the options and found out that option C satisfied both equations.

Guess like me.

Only joking Its the second one.

Simply substitute the values of x and y from the options the one which satisfies both the equations is the Sol

Substitute the values from the choices. EASY!

we can substitute reply from all multiple choice, and select which one is correct

for a easy way out, try putting all the given answers. whichever satisfies both equations is the solution.

x^4+5y=6 (1)

x^2.y^2+5x=6 (2)

eq (1) equal eq (2)

x^4+5y=x^2.y^2+5x x^4 - x^2.y^2 = 5(x - y) x^2.(x^2 - y^2) = 5.(x - y) x^2.(x - y).(x + y) = 5.(x - y) x^2.(x - y).(x + y) - 5.(x - y) = 0 (x - y).[ x^2.(x + y) - 5 ] = 0

x-y=0 so x=y (3) ----- or x^4 + 5x - 6 = 0 (x+2)(x-1)(x^2-x+3)=0 x = -2 or x = 1 and 2 imaginary roots

x = y = -2 x = y = 1