Just for fun!-XV
Evaluate the number of digits in 2 1 0 0
Note : You may use the fact that lo g 2 = 0 . 3 0 1 .
The answer is 31.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
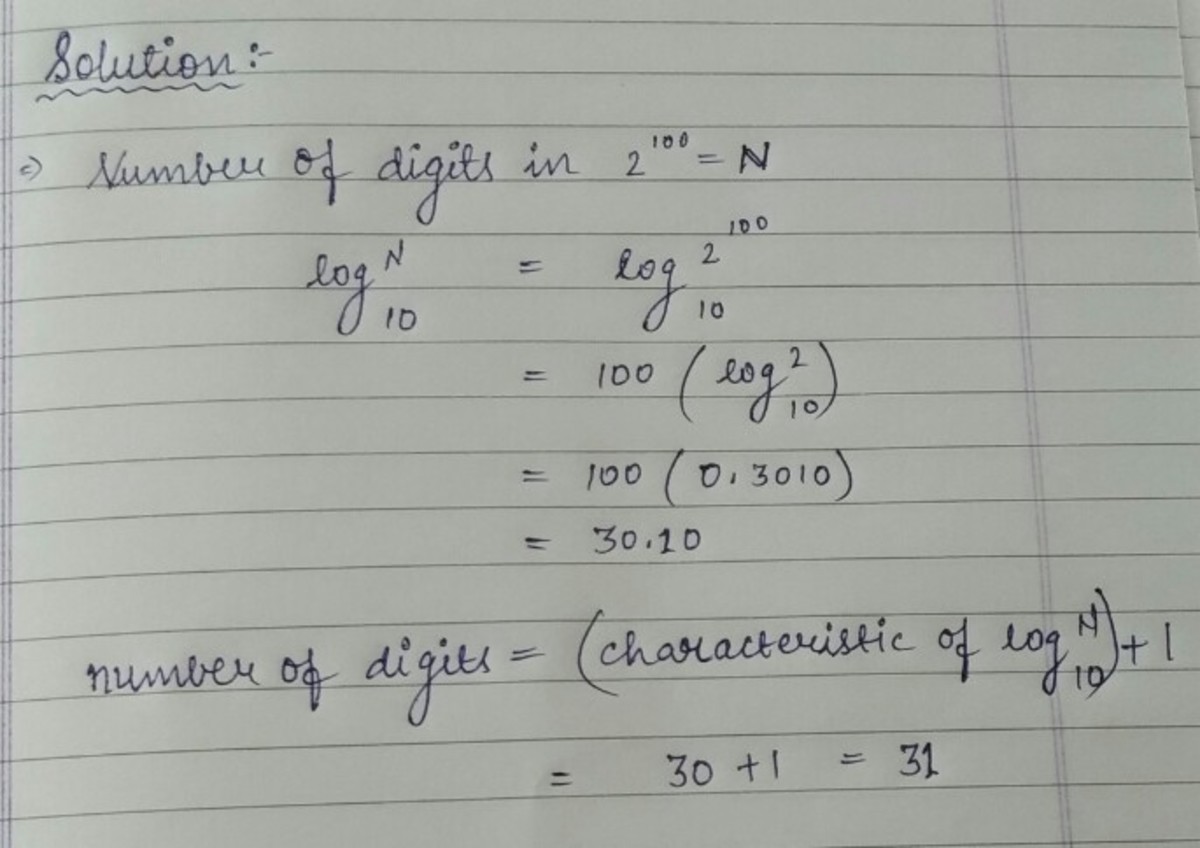
Awesome solution.Upvoted! ( Im pretty sure im not gonna stop mentioning this but awesome calligraphy)
Excellent solution.
Nice solution but for beginners, it would be better if you add a few lines on why is the number of digits in an exponent is ⌈ lo g N ⌉
It's the same method as the one posted by Raj. But for those who are new to these kind of problems I'd like to post a more detailed solution.
At first, let's take a look at some explicit examples :
Smallest 1 , 2 , 3 & 4 digit positive integer are 1, 10, 100 \text { &} \, 1000 respectively. Now, lo g 1 = 0 lo g 1 0 = 1 lo g 1 0 0 = 2 lo g 1 0 0 0 = 3 Notice that, for n digits it's always ( n − 1 ) . As, lo g x always increases as x increases towards positive infinity, it's always true that, for x to be a n digit positive integer, n − 1 ≤ lo g x < n ⇒ ⌊ lo g x ⌋ = n − 1 ⇒ n = ⌊ lo g x ⌋ + 1
Here, ⌊ . ⌋ represents the floor function. ⌊ x ⌋ is the greatest integer not greater than x . For example, ⌊ 3 . 9 8 ⌋ = 3 & ⌊ 4 ⌋ = 4
Thus, for this question, n = ⌊ lo g 2 1 0 0 ⌋ + 1 ⇒ n = ⌊ 1 0 0 lo g 2 ⌋ + 1 ⇒ n = ⌊ 1 0 0 × 0 . 3 0 1 0 ⌋ + 1 ⇒ n = ⌊ 3 0 . 1 ⌋ + 1 = 3 0 + 1 = 3 1
Thank you, for your detailed sollution..........
log 2¹⁰⁰ = 100 log 2 = 30.1 ... ... ... => 2¹⁰⁰ = 10^30.1 ... ... ... => 31 digit