Just for the isosceles?

Geometry Level 2

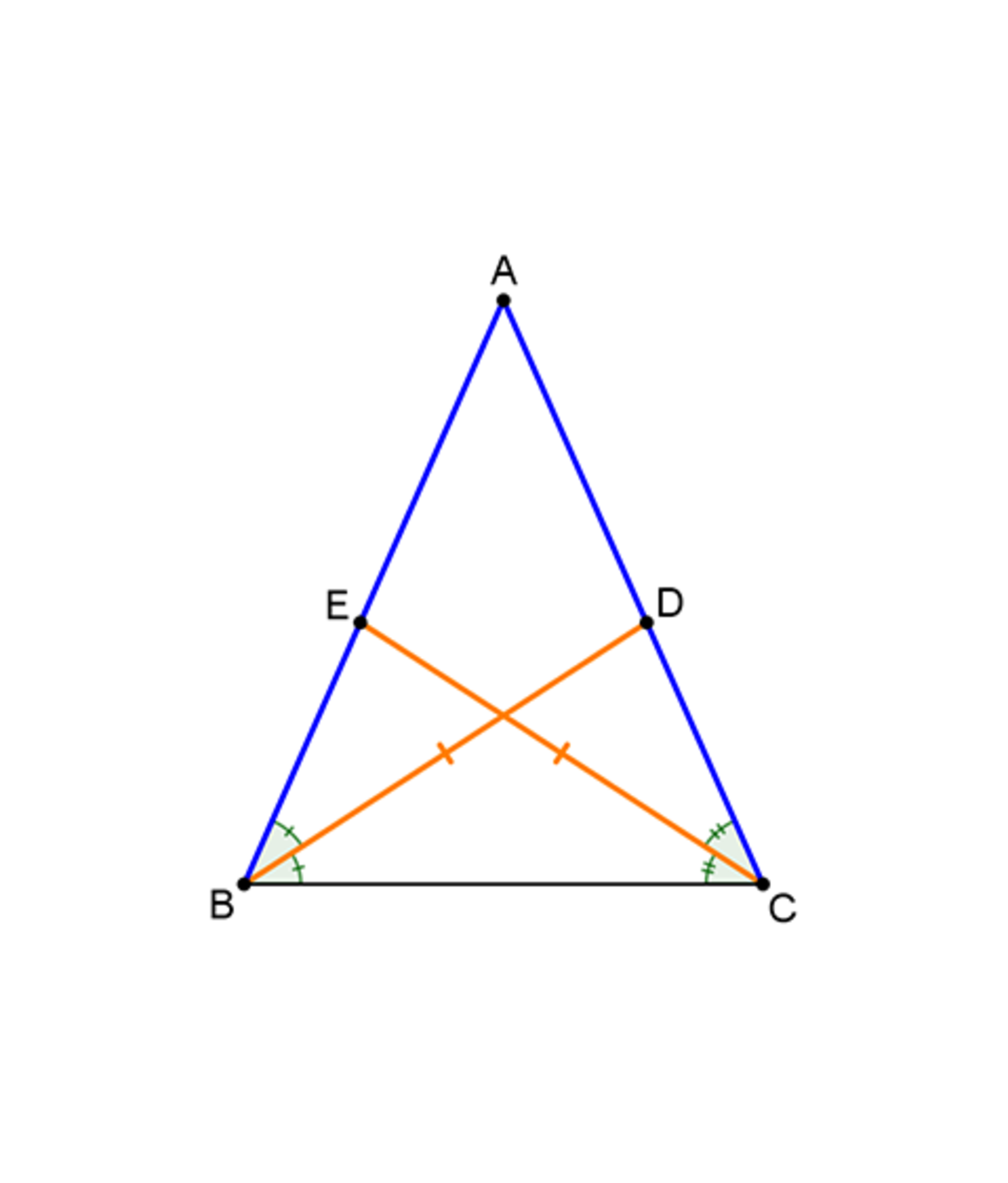It is easy to see that if two sides of a triangle are equal (i.e. if the triangle is isosceles), then the corresponding angle bisectors are equal as well.

What about the converse ?

In a given triangle A B C ABC , B D BD and C E CE are the angle bisectors of ∠ B \angle B and ∠ C \angle C respectively.

If ∣ B D ‾ ∣ = ∣ C E ‾ ∣ \left| {\overline {BD} } \right| = \left| {\overline {CE} } \right| , is it necessarily true that ∣ A B ‾ ∣ = ∣ A C ‾ ∣ \left| {\overline {AB} } \right| = \left| {\overline {AC} } \right| ?

Hint : Angle bisector theorem might be useful.

Cannot tell No Yes

Thanos Petropoulos by Thanos Petropoulos , 61, Greece

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Label ∣ A B ‾ ∣ = c \left| {\overline {AB} } \right| = c , ∣ A C ‾ ∣ = b \left| {\overline {AC} } \right| = b , ∣ B C ‾ ∣ = a \left| {\overline {BC} } \right| = a , ∣ A D ‾ ∣ = w \left| {\overline {AD} } \right| = w , ∣ C D ‾ ∣ = x \left| {\overline {CD} } \right| = x , ∣ A E ‾ ∣ = y \left| {\overline {AE} } \right| = y , ∣ B E ‾ ∣ = z \left| {\overline {BE} } \right| = z .

By angle bisector theorem, x w = a c \frac{x}{w} = \frac{a}{c} thus, x x + w = a a + c ⇒ x b = a a + c ⇒ x = a b a + c \frac{x}{{x + w}} = \frac{a}{{a + c}} \Rightarrow \frac{x}{b} = \frac{a}{{a + c}} \Rightarrow x = \frac{{ab}}{{a + c}} .

Similarly, w = c b a + c w = \frac{{cb}}{{a + c}} , y = b c a + b y = \frac{{bc}}{{a + b}} , z = a c a + b z = \frac{{ac}}{{a + b}} .

Moreover, ∣ B D ‾ ∣ 2 = a c − w x {\left| {\overline {BD} } \right|^2} = ac - wx and ∣ C E ‾ ∣ 2 = a b − y z {\left| {\overline {CE} } \right|^2} = ab - yz .

Since ∣ B D ‾ ∣ = ∣ C E ‾ ∣ \left| {\overline {BD} } \right| = \left| {\overline {CE} } \right| , combining we get:

a c − w x = a b − y z ⇒ a c − a b 2 c ( a + c ) 2 = a b − a b c 2 ( a + b ) 2 ac - wx = ab - yz \Rightarrow ac - \frac{{a{b^2}c}}{{{{\left( {a + c} \right)}^2}}} = ab - \frac{{ab{c^2}}}{{{{\left( {a + b} \right)}^2}}}

Rearranging, ( b − c ) ( a 2 + b 2 + c 2 + 2 a b + 2 b c + 2 c a ) = 0 \left( {b - c} \right)\left( {{a^2} + {b^2} + {c^2} + 2ab + 2bc + 2ca} \right) = 0 . The second factor is positive, hence b = c b = c . Correct choice: Yes \boxed{\text{Yes}}

5 Helpful 5 Interesting 5 Brilliant 1 Confused

How can I get |BD|^2=ac-wx?

wing yan yau - 1 year, 5 months ago

Log in to reply

It comes from the Angle Bisector Theorem. Check this wiki: https://brilliant.org/wiki/angle-bisector-theorem/

Thanos Petropoulos - 1 year, 5 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...