Just hangin' around ......
Suppose there are two (vertical) poles, one of height 1 0 0 feet and the other 7 0 feet, positioned a horizontal distance of 8 0 feet apart on level ground. A rope of length 1 0 0 feet connects the tops of the two poles. A weight, placed on the rope so that it can slide freely along it, is allowed to come to rest.
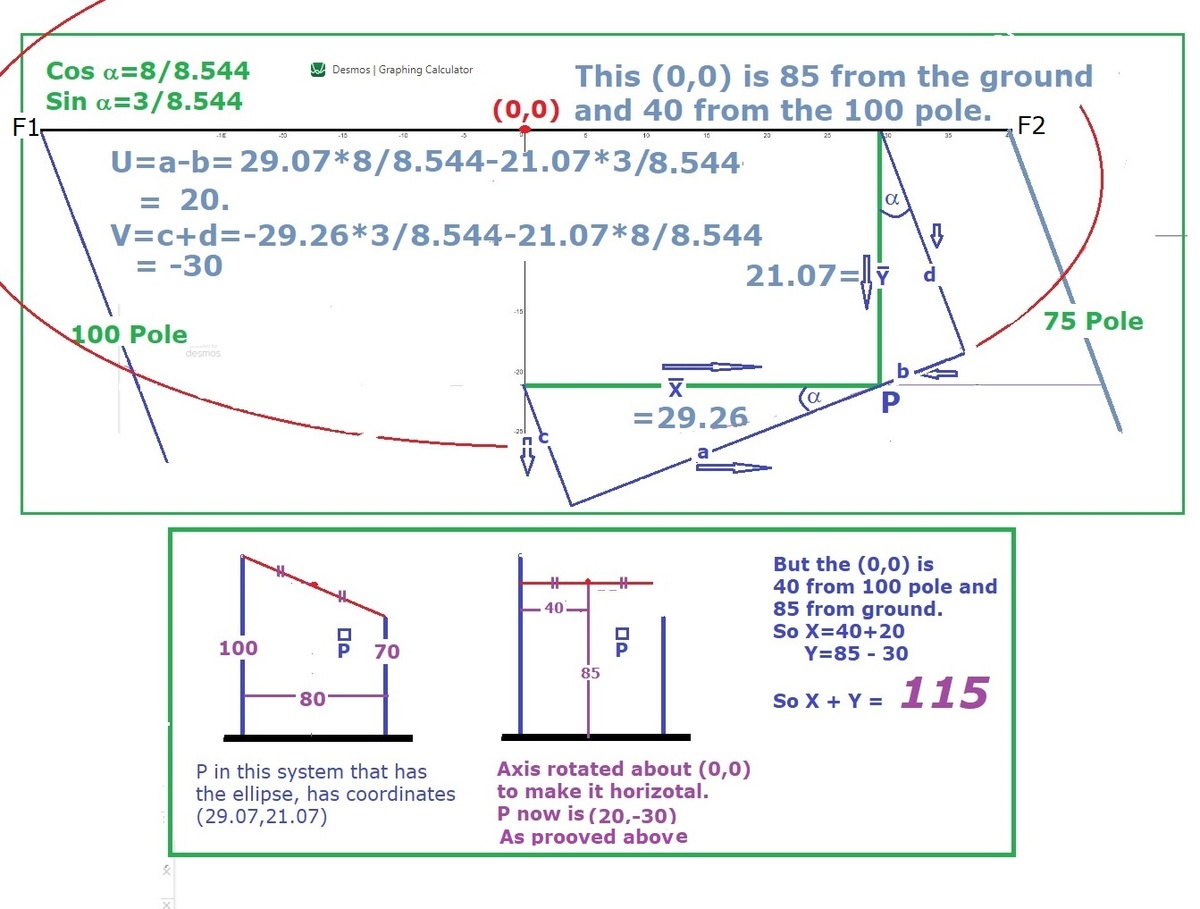
Once at rest, the weight is a horizontal distance X from the 1 0 0 foot pole and a vertical distance Y above the ground. Find X + Y .
Clarification: Assume that the rope forms a straight line from the weight to each of the pole tops.
The answer is 115.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
I missed it, was applying work-energy and all.
@Brian Charlesworth Your problems have a newness in them and your solution are short and simple.I want to write solution like you and @Chew-Seong Cheong.
u both also are my ideal in Brilliant. (^_^)
Nice problem. Glad it found its way back into circulation so I could see it
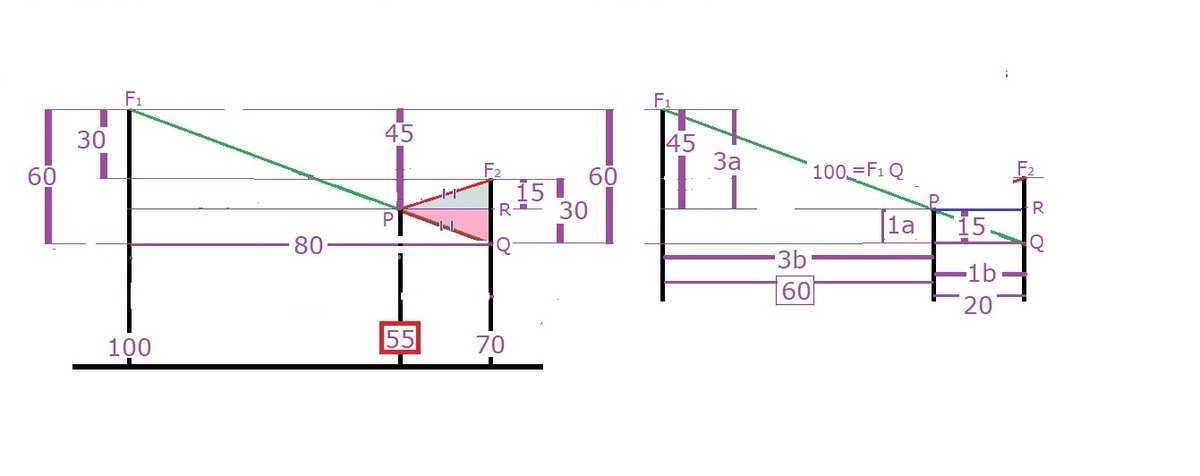
Sketch for the above simple beautiful solution.
If "Since tension through out the rope is same" is added, it may be simple for some to understand.
By the way the point is on an oblique ellipse. Only another method. Yours is the best AS NORMAL with you.

When the weight is at rest, the parts of the rope on the left and right of the weight has the same tension T and form a same angle θ with the vertical, so that it has zero resultant horizontal force T sin θ − T sin θ = 0 .
We note that the length of the rope is given by:
sin θ X + sin θ 8 0 − X = 1 0 0 ⇒ sin θ 8 0 = 1 0 0
⇒ sin θ = 1 0 0 8 0 = 5 4 ⇒ cos θ = 5 3 ⇒ tan θ = 3 4
We also note that:
⎩ ⎪ ⎨ ⎪ ⎧ tan θ = 3 4 = 1 0 0 − Y X tan θ = 3 4 = 7 0 − Y 8 0 − X ⇒ − 4 Y = 3 X − 4 0 0 ⇒ − 4 Y = 2 4 0 − 3 X − 2 8 0 = − 3 X − 4 0
Subtracting the two equations, we have:
6 X − 3 6 0 = 0 ⇒ X = 6 0
⇒ − 4 Y = 3 ( 6 0 ) − 4 0 0 ⇒ Y = 4 2 2 0 = 5 5
Therefore, X + Y = 6 0 + 5 5 = 1 1 5
My solution is a little bit brutal compared with Brian's elegant one.
Assuming that the tension in the rope is constant, the rope must make equal angles with the horizontal on either side of the weight. The two obvious right angled triangles are therefore similar, and we can say
1 0 0 − y x = 7 0 − y 8 0 − x
And using Pythagoras theorem twice we can write the total length of the rope as
x 2 + ( 1 0 0 − y ) 2 + ( 8 0 − x ) 2 + ( 7 0 − y ) 2 = 1 0 0
Asking Mathematica to solve these two equations simultaneously then gives ( x , y ) = ( 6 0 , 5 5 )
and so x + y = 1 1 5
Solve [ x 1 0 0 − y = 8 0 − x 7 0 − y ∧ EuclideanDistance [ { 0 , 1 0 0 } , { x , y } ] + EuclideanDistance [ { x , y } , { 8 0 , 7 0 } ] = 1 0 0 ∧ 0 ≤ x ≤ 8 0 ∧ 0 ≤ y ≤ 7 0 ] ⇒ x → 6 0 , y → 5 5 ⇒ 1 1 5 .
The first subexpression contains the information that the angles are equal, the second rope length and the third and fourth to preclude unreal answers.
A quick, cryptic solution ....
The rope will have the same slope on either side of the mass. This means that if the rope were to be extended downward from the top of the 1 0 0 foot pole along the same slope it will have descended 1 0 0 2 − 8 0 2 = 6 0 feet, i.e., 3 0 feet below the top of the 7 0 foot pole. By symmetry, the mass must then be a vertical distance of 2 3 0 = 1 5 feet below the top of the shorter pole, (and 4 5 feet below the top of the taller pole). Thus the mass will hang a vertical height of Y = 5 5 feet above the ground.
By way of similar triangles, the ratio of the horizontal distances of the mass from the taller and shorter poles will be 3 : 1 , implying that the mass will be a horizontal distance of X = 6 0 feet from the 1 0 0 foot pole.
We therefore have that X + Y = 1 1 5 .