Just hanging around , Medium part2
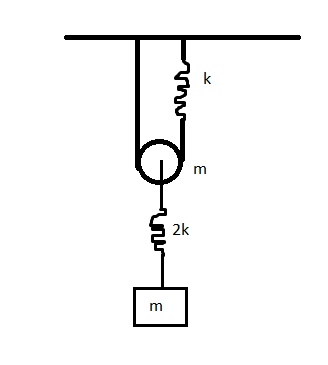
If the time period of SHM of rectangular block can be represented as T = 2 π b k a m . Find a 2 + b 2
Details
- The pulley is smooth with mass m , the strings are massless and inextensible.
- The two springs are in phase.
- The pulley system is in a uniform gravitational field.
- Zig-zag lines in fig represents spring of spring constant k and 2k as shown.
- a is of the form c + d where c is a square free integer. And b is of the form e f where f is square free integer.
-
The pulley and the block oscillate in phase with the same frequency
The answer is 13.82.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Exactly!!thank god u solved this in between so many reports and all of them say it is not specified that b a is in simplest form
Log in to reply
Hey... Please specifically mention that the sqrt(2) term needs to be cancelled from a and b.... I got a = 2 + sqrt(2) and b = 4... And the answer obviously doesn't match!!
Log in to reply
Please read the question again.It is specified that is of form c + d
Can u please post a easy solution
Log in to reply
Yup, that's why ∣ N 1 ∣ = k ⋅ ( 2 y 1 ) = 2 k y 1 ...
How could you tell that α = ω 4 − 2 2 is the required root here? Which additional conditions imply this? Thanks. :)
Here, we assume that both, the block and the pulley oscillate in the same phase i.e. Y1=A exp(iαt) and Y2=B exp(iαt). Y2 can be equal to B*exp(i(αt+Φ)). Please explain how this assumption is valid.
Good explanation.
Why is it necessary for the pulley and the block to oscillate with same frequency???
If displacement of pulley is y then extension in spring k must be 2y
Let y 1 ( t ) and y 2 ( t ) be distances of pulley and mass respectively from their initial positions (wheh both springs are not deformed). We say that y 1 ( t ) (and y 2 ( t ) too) is greater then zero iff it is below its initial position. We can easily observe that the extension of spring k is equal y 1 and for 2 k it is y 2 − y 1 . If we denote by N 1 tension in above string and N 2 is the second one, we get from second dynamics law: m g + N 2 − 2 N 1 = m y ¨ 1 , m g − N 2 = m y ¨ 2 . It is easy to notice, that due to assumed signs there is N 1 = 2 k y 1 and N 2 = 2 k ( y 2 − y 1 ) . So we have a system of differential equations. Observe that we don't need to solve it but only to find angular velocity ω . The angular velocity doesn't depend on constant components, therefore we can consider the following system N 2 − 2 N 1 = m y ¨ 1 , − N 2 = m y ¨ 2 and therefore 2 k ( y 2 − y 1 ) − 4 k x 1 = m y ¨ 1 , − 2 k ( y 2 − y 1 ) = m y ¨ 2 . In general the motion is a superposition of simple harmonic motions (normal modes) of both bodies. That's why we look for solutions of the form y 1 = A e i α t and y 2 = B e i α t (to be honest we are not sure that such a motion exists but we can try it and indeed there will be a general solution). Moreover we substitute ω 2 = m k and we have 2 ω 2 ( B − A ) − 4 ω 2 A = − α 2 A , − 2 ω 2 ( B − A ) = − α 2 B . After writing it in a matrix form and computing the determinant of 2 × 2 matrix which must be zero (for nonzero A,B) we have α 4 − 8 α 2 ω 2 + 8 ω 4 = 0 so α 2 = ( 4 ± 2 2 ) ω 2 . We observe that the motion is a linear superposition of e i α for all α but since we have SHO, there is only one α 2 allowed. Now it easy to conclude (due to additional conditions) that there must be α = ω 4 − 2 2 what (with α = 2 π T 1 ) lead us to T = 2 π 2 2 1 + 2 k m and for a = 1 + 2 , b = 2 2 we get a 2 + b 2 = 1 1 + 2 2 which is a solution.