Just know the diagonal . .
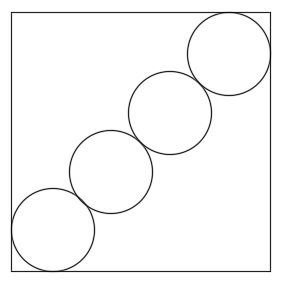
The four circles shown above are identical and their diameters lie on the diagonal of the square. Find the ratio of the area of the square to the area of the four circles. If your answer can be expressed as where and are positive coprime integers, give your answer as .
The answer is 19.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
First of all, the point where the two middle circles are tangent is the center of the square. Thus, if we assume the square has a side length of one, the distance from the center of the square to the bottom left vertex is 2 2 . Next, draw perpendicular's from the bottom most circle's radius, which I will name O , to its points of tangency with the square. Realizing that these perpendiculars are equal in length because they are radii, the distance from O to the corner of the square must be 2 r where r is the radius of the individual circles. Therefore, 3 r + 2 r r ( 3 + 2 ) r = 2 2 = 2 2 = 1 4 3 2 − 2 Then, solving for area of all four circles leads to A 1 A 1 A 4 = ( 1 4 3 2 − 2 ) 2 π = 9 8 1 1 − 6 2 π = 4 9 2 2 − 1 2 2 π The ratio of the square's area to the area of the four circles is then 4 9 2 2 − 1 2 2 π 1 = 2 π 1 1 + 6 2 This implies then that a + b + c = 1 1 + 6 + 2 = 1 9 .