Just one step to regularity of quadrilateral
Let ABCD be a convex quadrilateral. Also let P, Q, R, S be the respective midpoints of sides AB, BC, CD, DA such that triangles AQR and CSP are both equilateral.
Find the largest angle (in degrees) of quadrilateral ABCD.
The answer is 120.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Moderator note:
This is definitely one of those problems where the numerical value is easier to get than the full proof that it's optimal!
How did you draw the last conclusion
Log in to reply
The points of the perfect star form the regular hexagon S A P Q C R . The angles ∠ S A P = ∠ Q C R are both angles of the both quadrilateral and of the hexagon, therefore the largest angle of the quadrilateral is 1 2 0 ∘ . The remaining angles must be smaller, 6 0 ∘ each.
@Marta Reece Since the problem has got enough popularity, I would like to ask you to clarify why D B passes through the intersections of the both equilateral triangles. This is an R M O problem, so give a perfect m a t h e m a t i c a l explanation. As your last conclusion that S A P Q C R is a regular hexagon is totally dependent on your assumption that D B passes through the intersections of the both equilateral triangles. Thanks.
Since the problem is asking for the greatest angle in the quadrilateral, I think we have to question symmetry. Can AB, BC, CD, AD have different lengths? Why MUST SP and RQ be parallel? If we move B away from O, arbitrarily some where AB < BC , PQ might != SR; SP and RQ will not be parallel; and it is not yet known that the equalateral triangles CSP and AQR are the same size.
Log in to reply
The four sides of the quadrilateral have to be shown to have the same lengths. Part of that process is showing that SP and RQ are parallel. This is done using the triangle ABD. S and P are midpoints of the sides AD and AB respectively. This means SP has to be parallel to DB. By the same type of argument for triangle CBD the segment RQ has to be parallel to DB. So if the two segments are both parallel to DB, they are parallel to each other. And the triangles are the same size, because the midpoint connections are the same size, being each half as big as DB, and they are each a size of one of the triangles. The only way we can move B away from so that AB<BC would be to slide the the triangle ARQ with it half as far. But then point P would no longer be half way between A and B, as it is required to be. So the symmetry is there and the sides are the same length.
If we consider one equilateral triangle to be a
1
8
0
∘
rotation of the other, then we can move one triangle up or down to create different quadrilaterals:
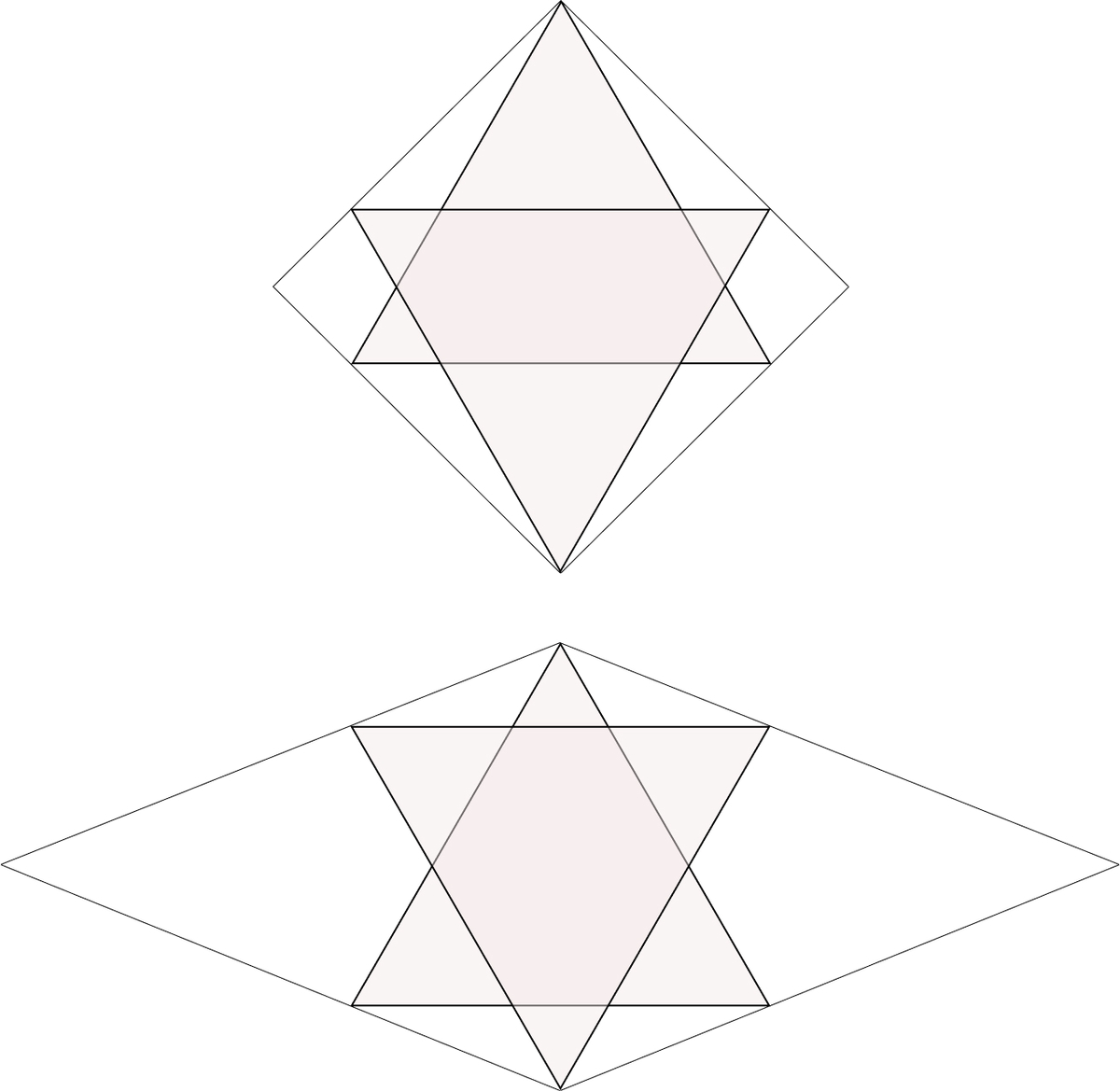In the first case, the two triangles are too far apart, and the lengths of the quadrilateral are not bisected.
In the second case, the two triangles are too close together, and again the lengths of the quadrilateral are not bisected.
There must exist a point in between, where the lengths of the quadrilateral are bisected.
The solution from @Marta Reece shows that this must be the arrangement where the centroids of the triangles overlap.
From there, the upper angle of the quadrilateral must be partitioned into 3 0 ∘ , 6 0 ∘ and 3 0 ∘ = 1 2 0 ∘ .
Your argument shows that if you pick symmetrically arranged equal sized equilateral triangles, you will find a solution by sliding them along the vertical axis. It does not show that they have to be symmetrically arranged and equal sized to provide a solution.
Log in to reply
And for that reason I referred to your solution, which was the same as mine:)
Dan ley, can u please tell me about your qualifications.For every problem u give your extraordinary solution.I am now in class 10th(15 years old) and I wanted to know your
qualifications because I too wanted to be like you.
So I request you, please tell your qualification.
Log in to reply
Thank you! I've gone through the English schooling system (done GCSEs and have almost finished my A-levels). But I did very little maths until last year, so you've got plenty of time to keep practicing! In general, just keep challenging yourself. Brilliant's a great place for it- have a go at writing some solutions too?:)
@Dan Ley The points P , Q , R and S are the midpoints of the quadrilateral. In that case Marta is totally correct.
Log in to reply
Yes for sure!:) This is by no means a complete solution, it just reasons that this is a possible solution, and Marta's solution does the specifics, which I thought would be boring to repeat.
Why should we consider one triangle to be a 180 degree rotation of another?
In my earliest (failed) attempts to answer this problem I assumed the angle between the triangles could be a variable which eventually 'cancelled out' to produce a unique answer. I quickly found that there had to be a kind of rotational symmetry where the internal angles of the central hexagon were A, B, A, B, A, B but it was not at all obvious that angle A equalled angle B.
The easy way to solve this problem is to place the two triangles into the most symmetrical position relative to each other and check that the quadrilateral enclosing the resulting regular six-pointed star does satisfy all the requirements.
Showing that it is the only solution takes a little longer.
S P has to be parallel to D B because points S and P are midpoints of A D and A B respectively. Similarly R Q is parallel to D B , so S P is parallel to R Q , which means the two equilateral triangles are rotated exactly the 1 8 0 ∘ relative to each other.
The same midpoints give us S P = 2 1 D B , and R Q = 2 1 D B , so two equilateral triangles are the same size.
Similarity of △ A S P and △ A D B , and consequently also △ A T P and △ A O B , guarantees that A T = T O , since A P = P B . That means the equilateral triangles are in the correct position vertically to form the star.
And similarity of △ O B C and △ U B Q guarantees that O U = U B because C Q = Q B , that is the equilateral triangles are not offset horizontally.
So we conclude that the two triangles △ S P C and △ A Q R do indeed form a perfect six-pointed star, and the largest angle of the quadrilateral is therefore the internal angle of the regular hexagon formed by the points S A P Q C R , or 1 2 0 ∘ .