A geometry problem by Prayas Rautray

Geometry Level 3

Let $\triangle ABC$ be an acute angled triangle and $CD$ be the altitude through $C$ . If $AB=8$ and $CD=6$ , find the distance between the midpoints of $AD$ and $BC$ .

The answer is 5.

2 solutions

Ahmad Saad
Aug 26, 2017

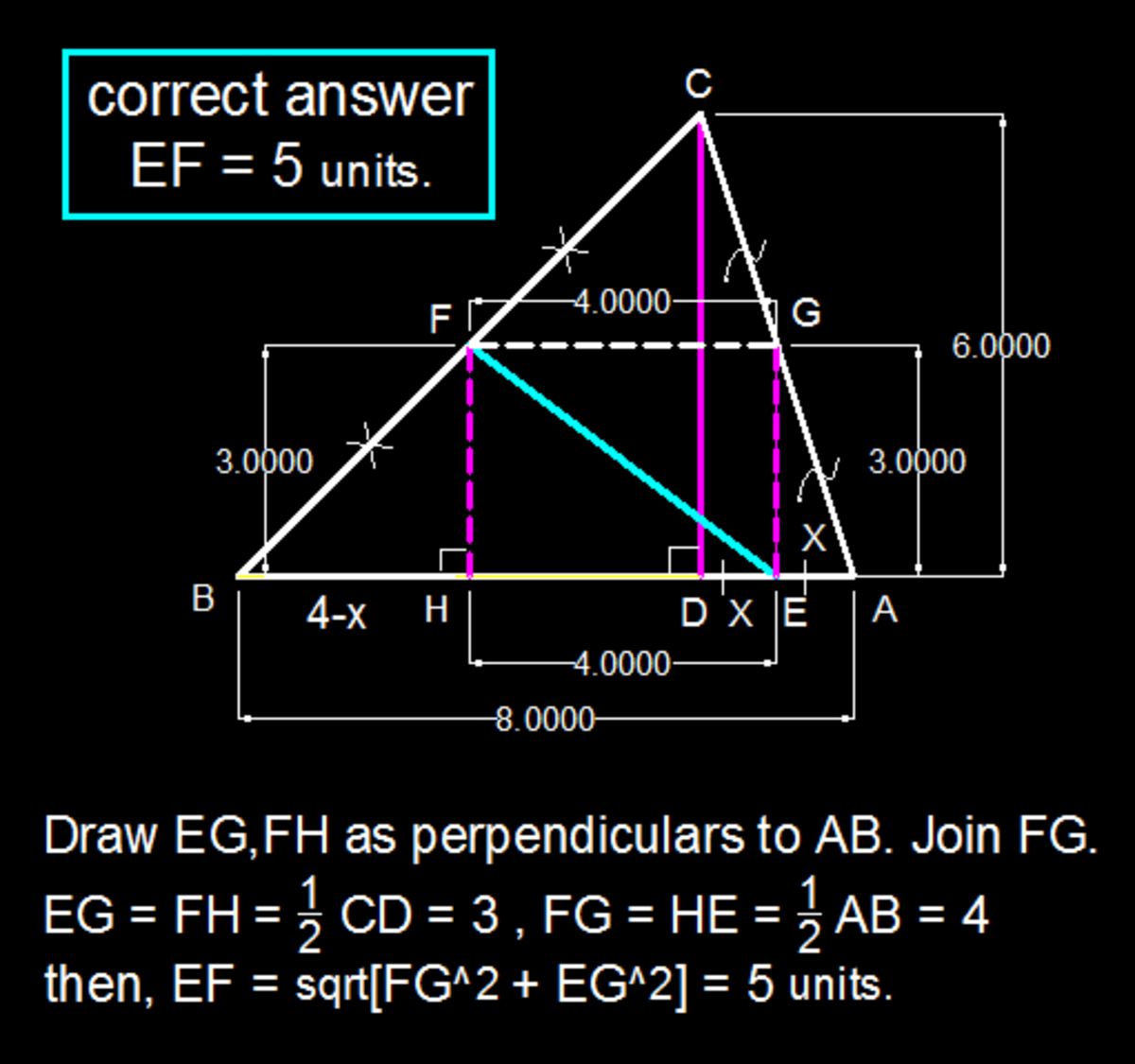
@Ahmad Saad , we really liked your comment, and have converted it into a solution. If you subscribe to this solution, you will receive notifications about future comments.

Brilliant Mathematics Staff - 3 years, 9 months ago

Marta Reece
Aug 26, 2017

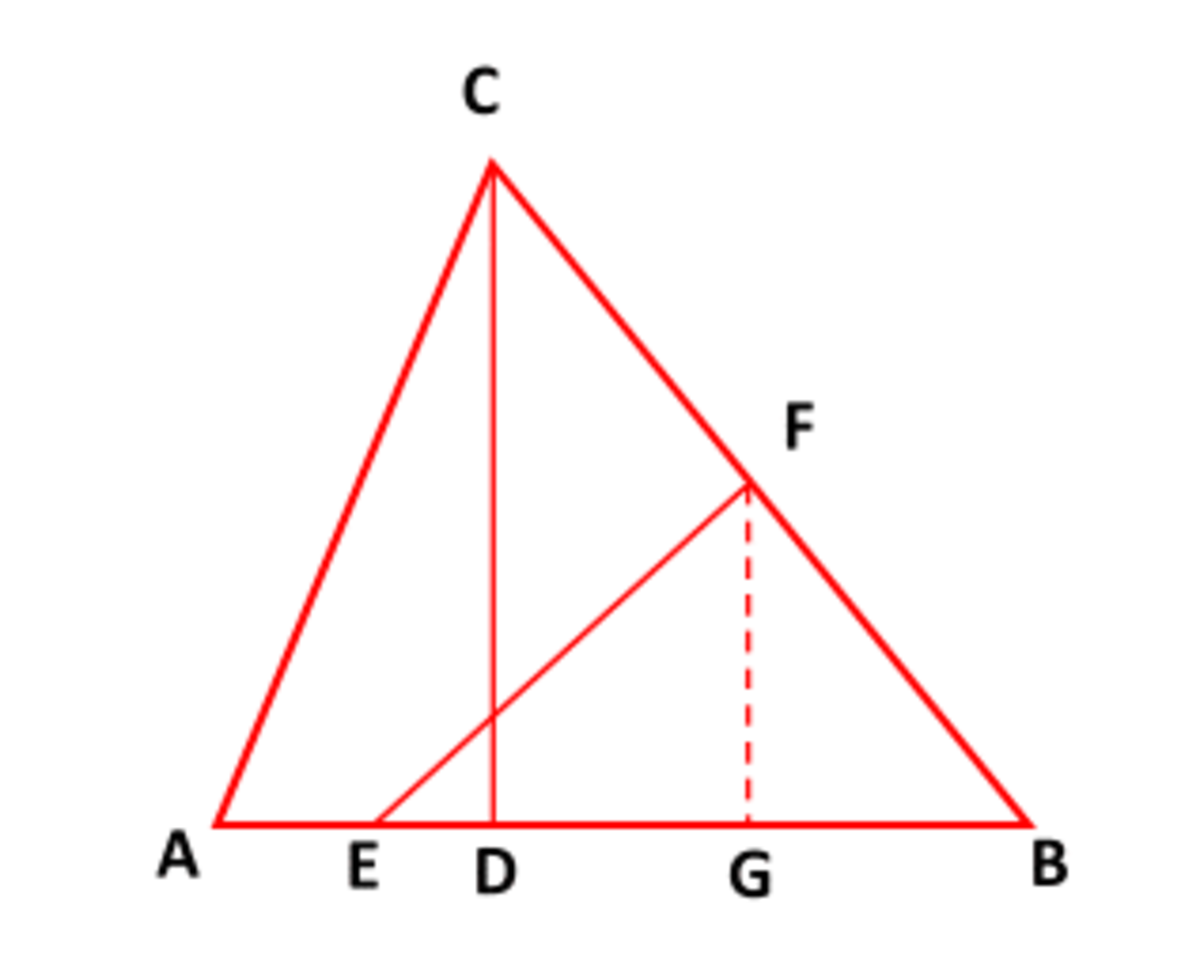If $CD=6$ and $F$ is midpoint of $BC$ , then $FG=3$ .

$AB=8=AD+DB$

$ED=\frac12AD$ and $DG=\frac12DB\implies EG=\frac12(AD+DB)=\frac12 AB=4$

Distance $EF=\sqrt{3^2+4^2}=\boxed5$

@Marta Reece , we really liked your comment, and have converted it into a solution. If you subscribe to this solution, you will receive notifications about future comments.

Brilliant Mathematics Staff - 3 years, 9 months ago

A geometry problem by Prayas Rautray

The answer is 5.

2 solutions

0 pending reports