Just Some Altitudes
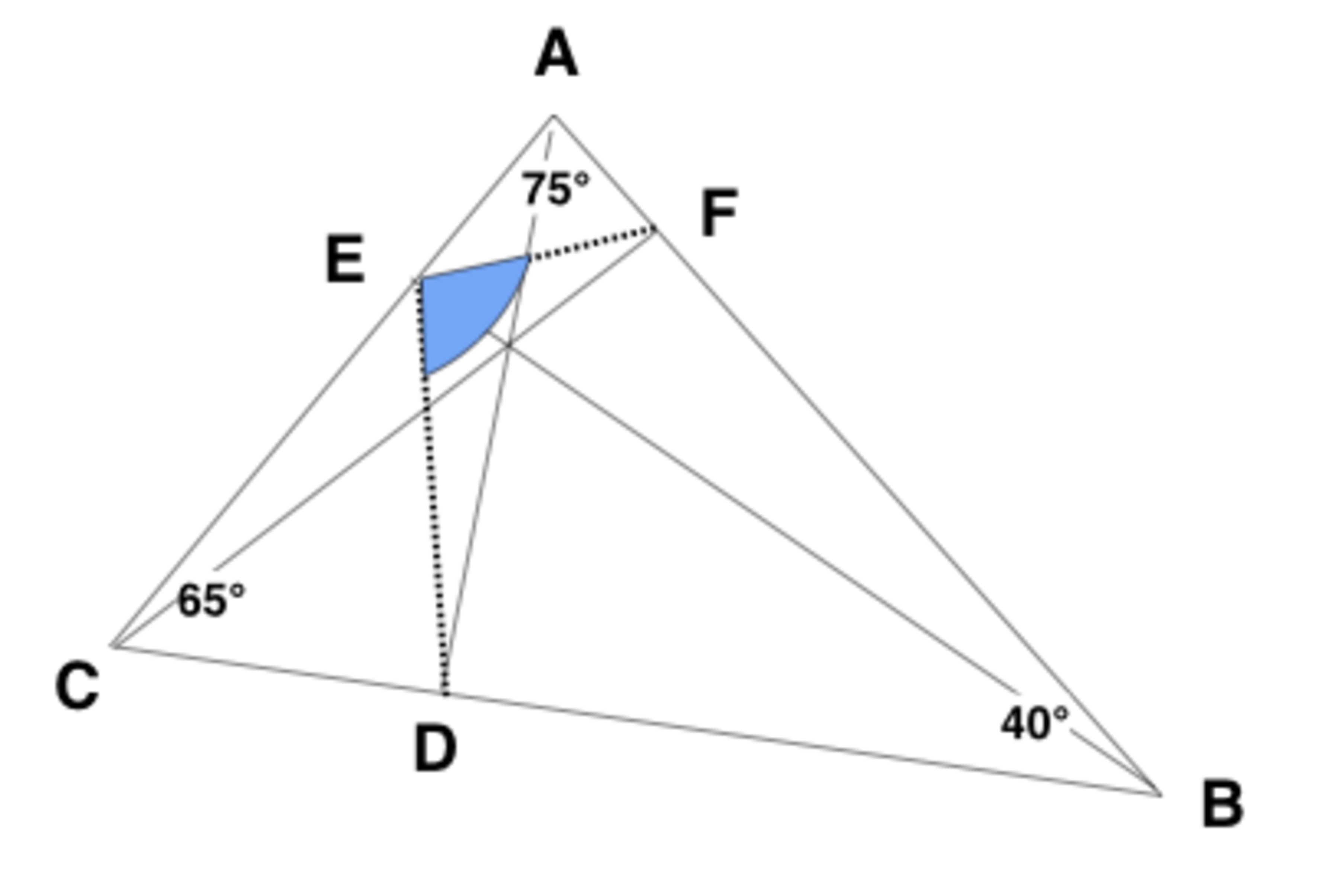
are the feet of the altitudes in triangle Find (in degrees).
The answer is 100.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let H be the orthocenter of A B C . Then, since ∠ A E H = ∠ A F H = 9 0 ∘ , quadrilateral A E H F is cyclic . Equivalently, we can find that B F H D and C E H D are cyclic as well.
Consider the circumcircle about A E H F . We see that ∠ H E F = ∠ H A F since they subtend the same arc. Similarly, ∠ F C D = ∠ D E H . Finally, ∠ H A F = ∠ F C D since △ H F A ∼ △ H D C . Thus, ∠ H E F = ∠ F C D = ∠ D E H ; in other words, B E bisects ∠ D E F .
This gives ∠ D E F = ∠ H E F + ∠ D E H = 2 ∠ H E F = 2 ( 9 0 ∘ − ∠ A B D ) = 2 ( 9 0 ∘ − 4 0 ∘ ) = 1 0 0 ∘ .
Remark: There might be a more obvious way to see that B E bisects ∠ D E F . Does anyone see such an approach?