Just some Limit

Calculus Level 2

$f\left(x\right)=\frac{x\ln\left(x\right)-\ln\left(x\right)}{9x^{2}-2e^{x}x-9x+2e^{x}}+2$

$g\left(x\right)=\sin^{2}\left(\frac{\pi x^{2}}{2}\right)$

$\lim_{x \rightarrow 1} \frac{f(x)}{g(x)}$

2 1/3 3 2/3

2 solutions

คลุง แจ็ค
Jan 3, 2020

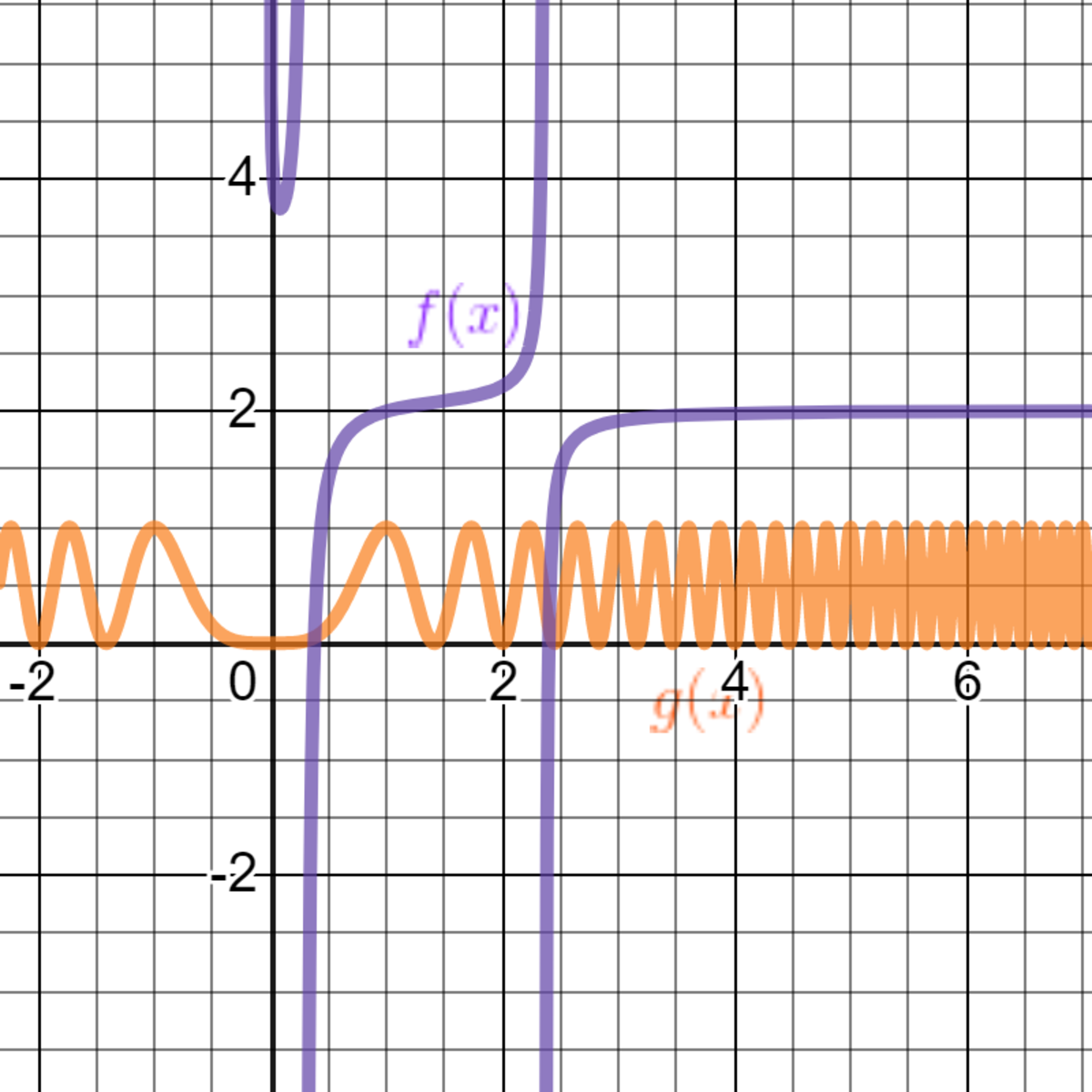
One can approach this directly.

First of all, $g(x)$ is continuous at x=1, so, we can just substitute $g(1)$

Next, consider $f(x)$ when x approaches 1,

$(x-1) \ln(x)$ tends to 0 as $(x-1)^{2}$ as x tend to 1 but the denominator tend to 0 as $(x-1)$ , so, the whole terms tends to 0. This can be proven very easily by Taylor's expansion.

So, the answer is $2$

S. P.
Jan 3, 2020

If you view f(x) & g(x) graphically, the limits become apparent.

Just some Limit

2 solutions

0 pending reports