Just a classic Rotational Motion Problem

Classical Mechanics Level 5

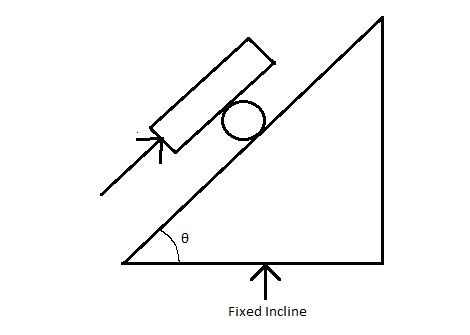A solid cylinder of mass M and radius R is rolled up on an incline with the help of a plank of mass 2M as shown in the figure.A constant force F is acting on the plank parallel to incline. There is no slipping at any of the contact. All surfaces are rough. The force of friction between the plank and cylinder is given by

$\displaystyle{\frac { aF+bMgsin\theta }{ c } }$

Find least value of $a+b+c$

Details

$\bullet$ Here $a,b,c$ are positive integers.

The answer is 24.

1 solution

Gautam Sharma
Mar 21, 2015

Let $f_1 ,f_2$ be the friction forces between plank and cyl. and cyl & wedge respectively.

For plank

$F-f_1-2Mgsin\theta =2Ma_1$

For cyl.

$f_1-f_2-Mgsin\theta =Ma_2$

R $(f_1+f_2)=I\alpha$

$(f_1+f_2)= \frac{Ma_2}{2}$

$also \quad a_1=a_2 +R\alpha$

$R\alpha =a_2$

Hence solving all these equations we get

$f_1=\frac{3F+2Mgsin\theta}{19}$

So $3+2+19=24$

awesome solution!!! did the same way.

A Former Brilliant Member - 3 years, 5 months ago

how's ur prep goin' ? :)

Shubham Dhull - 3 years, 5 months ago

fine....just trying to clear backlogs. How are things at your end? how's college?

A Former Brilliant Member - 3 years, 5 months ago

Just a classic Rotational Motion Problem

The answer is 24.

1 solution

0 pending reports