Just the Right Number to Find!

Notice that the difference between the number and respective remainder is equal.

$15 - 5 = 10, \, 25 - 15 = 10, \, 35 - 25 = 10.$

First, the $\text{LCM}$ of $15$ , $25$ and $35$ will be calculated which is $525$ .

Then We subtract from it the common difference, that is $10$ .

Hence $525 - 10 = 515$

Therefore the final answer is $\Large \displaystyle \color{#3D99F6}{\boxed{515}}$ .

Let X be the number

X must be 5 mod 15, 15 mod 25, and 25 mod 35

Then X can b expressed as: 15a+5, 25b+15, 35c+25

X = 15a+5=25b+15 = 35c+25

15a+5 = 35c+25 ...(1)

15a= 35c+20

3a= 7c+4

a= $\frac{7c+4}{3}$

7c+4 must be 0mod3

7c+4= 0mod3

c+1=0mod3

25b+15 = 35c+25 ...(2)

5b= 7c+2

b= $\frac{7c+2}{5}$

7c+2 must be 0mod5

7c+2= 0mod5

2c+2= 0mod5

c+1= 0mod 5

Since c+1=0mod3and c+1= 0mod 5, then c+1 must be 0mod 15.

The smallest possible c is 14.

Substituting c=14, X= $\boxed{515}$

Let x be the number that satisfies the given condtitions.

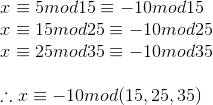
Since the LCM of 15, 25, 35 is 525, the least possible positive integer x is 525 - 10 = 515 .