Just The Series-Parallel Combinations
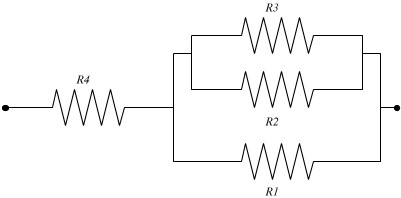
What is the maximum number of ways for four differently valued resistors to be arranged in a network that will result in distinct values?
Details:

The four resistors arranged in series in whatever order only gives one same value. So that is counted as one way.
The answer is 52.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
In my investigation, there are 1 0 ways to wire four resistors in different series-parallel combinations. Somehow, it is related to the number of partitions of 4, and each partition having two variants. I will be adding the pictures later as I am on my mobile device as of the moment.
4 has 5 partitions
4
3+1
2+2
2+1+1
1+1+1+1
If we treat the individual numbers as the number of resistors in a parallel subnetwork and the addition operation as placing these networks in series, we get 5 different patterns. If we interchange the treatments, we get another 5 patterns.
In each way, there are different number of permutations allowing for different values given differently valued resistors.
To lessen confusion, let us name the arbitrary resistors in each combination as p , q , r and s .
Way # 1. All resistors in series (form p+q+r+s.)

Here, no matter what arrangement of the resistors A , B , C , and D are, the equivalent resistance is the same.
= 1 combination
Way # 2. One parallel pair in series with the others (form p+q + r||s)
Here, we take into account the number of possible pairs from {A,B,C,D} which will be the parallel pair. That is 4 C 2 = 6 . We no longer take the arrangements of the remaining resistors in series, the arrangement of the resistors in parallel, and the position in the parallel pair as it does not give a change of value in the net resistance.
= 6 combinations
Way #3.
One resistor in series with a parallel network of two resistors in series and a resistor ( form p+ (q+r)||s)
There are 4 different ways of having the sole resistor in parallel, and with the remaining 3 resistors, there are 3 C 2 = 3 ways of selecting the two resistors in series to be paralleled with the firstly chosen resistor. That gives us 3 × 4 = 1 2 combinations.
= 12 combinations.
Way #4. 3 resistors series in parallel with a resistor (form (p+q+r)||s)
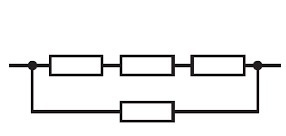
There are 4 ways of selecting the sole resistor in the parallel pair. Thus there are four distinguishable resistance networks of this form with differing values.
= 4 combinations
Way #5. Two resistors in series in parallel with the other two resistors in series (form (p+q)||(r+s))
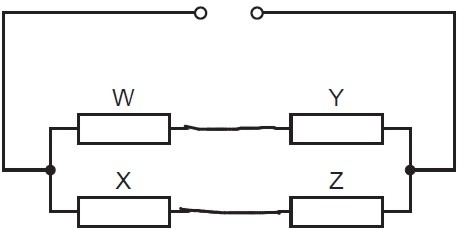
Here, there are just three configurations, as if we count 4 C 2 ways of pairing the resistor in one branch of the network (the other being automatic), then each configuration is counted twice. Thus there are only 3 combinations of this form.
= 3 combinations.
Way #6.
Three resistors in parallel with one another, in series with the fourth resistor (form (p||q||r) + s)
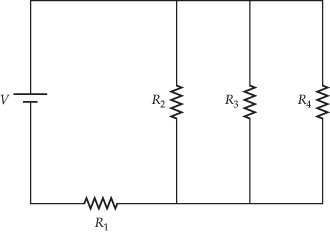
This is the direct complement of Way #4. (Notice how the "parallel" and "series" operators are swapped). Surprisingly, this also gives us just 4 ways, following the analysis given in Way #4.
= 4 combinations.
Way #7.
A resistor in parallel with a parallel pair and a resistor in series [ form p||((q||r) + s) ]
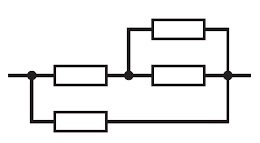
Again, this is a direct complement of Way #3 . Counting the same way, we also get 12 combinations.
= 12 combinations.
Way #8.
Three parallel networks (two resistors individually, and two resistors in series). (form p||q||(r+s) )
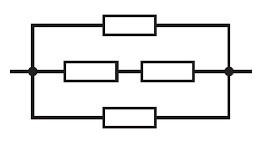
You could've guessed it. This is complementary to Way #2 . Again, there are 6 ways to have differently valued networks in this form.
= 6 combinations.
Way #9
. Two parallel networks in series. ( form (p||q) + (r||s) )
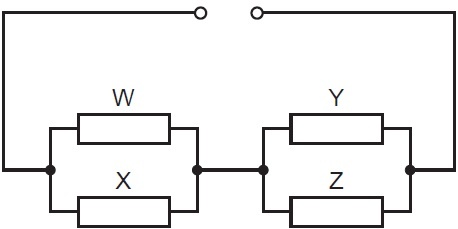
Similar to Way #5 , there are only three ways to have this form.
= 3 combinations.
Way #10. All in parallel with one another.
Well, this also is similar to Way #1 . No matter what order the resistors are, it gives the same net value, thus providing us just 1 combination.
= 1 combination.
So, summing it up, we get 5 2 .
Nice problem combining physics and combinatorics. I got the answer and what you intended for the problem, but there seems to be one minor issue. Just because all values of R1,R2,R3 and R4 are different, doesn't mean all 52 configurations you listed will have distinct resistance values.
For example, in way #5 and #9, if W = 1, X = 2, Y = 5, Z = 10, both configuration will give the same overall resistance of R = 4. So I think we need to change the wording a little bit, maybe the "maximum possible number of configurations with distinct resistance values"?
Log in to reply
Upon checking, yes! They do have the same results. But I guess that doesn't hold for all quadruples. Somehow, it might confuse the solvers, so I'll have to owe this one to you. Thank you for noticing that!
The possible combinations that are "series" on the highest level are ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ R 1 = a + b + c + d R 2 = ( a ∣ b ) + c + d R 3 = ( a ∣ b ∣ c ) + d R 4 = ( a ∣ b ) + ( c ∣ d ) R 5 = ( ( a + b ) ∣ c ) + d 1 6 4 3 1 2 with + for series, and | for parallel. The numbers indicate how many alternatives can be made be permuting a , b , c , d . By creating the dual circuits (interchanging series and parallel) we double the number of possibilities. This accounts for 2 × 2 6 = 5 2 different arrangements.
The bigger challenge is to prove that the 52 circuits can all have different values. This can be shown as follows.
Step 1 : Suppose all four resistors have the same value, a = b = c = d = r . Then the resistance depends only on the general geometry of the circuit. For the five patterns given above we get R 1 = 4 r ; R 2 = 2 2 1 r ; R 3 = 1 3 1 r ; R 4 = r ; R 5 = 1 3 2 r . The resistances of the dual circuits follow immediately: R 1 ⋆ = 4 1 r ; R 2 ⋆ = 5 2 r ; R 3 ⋆ = 4 3 r ; R 4 ⋆ = r ; R 5 ⋆ = 5 3 r . Thus the different shapes of circuits have different resistors except those of the form R 4 = ( a ∣ b ) + ( c ∣ d ) = r and R 4 ⋆ = ( a + b ) ∣ ( c + d ) = r . However, an infinitesimal change in a will guarantee that they are different. If we set a = r + ϵ , the resistances become R 4 = ( a ∣ b ) + ( c ∣ d ) = 4 + 2 ϵ 4 + 3 ϵ r ; R 4 ⋆ = ( a + b ) ∣ ( c + d ) = 4 + ϵ 4 + 2 ϵ r , which are clearly different.
Step 2 : Now make slight changes in the values so that a < b < c < d , but small enough so that the overall resistance changes by less than 6 1 r . This guarantees that the conclusion from Step 1 is still valid.
Using x ∣ ( y + z ) < y ∣ ( x + z ) and x + ( y ∣ z ) < y + ( x ∣ z ) iff x < y , we see that e.g. a + b + ( c ∣ d ) < a + c + ( b ∣ d ) < a + d + ( b ∣ c ) , b + c + ( a ∣ d ) < b + d + ( a ∣ c ) < c + d + ( a ∣ b ) , and similar comparisons apply to the other geometries. In this example, we have no way to compare a + d + ( b ∣ c ) and b + c + ( a ∣ d ) ; however, when increasing a infinitesimally to a + ϵ , the former value increases by ϵ while the latter increases by d 2 / ( a + d ) 2 ϵ < ϵ . Thus we can always make small adjustments in the value of a to guarantee the two are different.