Just the sides given, can you find the angle?
In △ A B C , if
a 4 + b 4 + c 4 = 2 c 2 ( a 2 + b 2 ) ,
then the possible measure(s) of ∠ C could be __________ .
Details and Assumptions:
-
a , b , c are the sides of △ A B C opposite to ∠ A , ∠ B , ∠ C respectively.
-
∠ C is measured in radians .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I did the same, although I complicated a bit more by isloating C with bhaskara...
We can use Heron's formula expressed in another way, to find the area of △ A B C :
4 [ A B C ] = ( a 2 + b 2 + c 2 ) 2 − 2 ( a 4 + b 4 + c 4 )
Now, we substitute the expression we are given:
4 [ A B C ] = ( a 2 + b 2 + c 2 ) 2 − 4 c 2 ( a 2 + b 2 )
Try to simplify it:
4 [ A B C ] = a 4 + b 4 + c 4 + 2 a 2 b 2 + 2 a 2 c 2 + 2 b 2 c 2 − 4 a 2 c 2 − 4 b 2 c 2 4 [ A B C ] = a 4 + b 4 + c 4 + 2 a 2 b 2 − 2 a 2 c 2 − 2 b 2 c 2 4 [ A B C ] = ( a 2 + b 2 − c 2 ) 2 4 [ A B C ] = ∣ a 2 + b 2 − c 2 ∣
Now, by law of sines, we now that [ A B C ] = 2 a b sin ∠ C , so sin ∠ C = a b 2 [ A B C ] , and substituting the area:
sin ∠ C = 2 a b ∣ a 2 + b 2 − c 2 ∣
By law of cosines, we know that cos ∠ C = 2 a b a 2 + b 2 − c 2 , and since a and b are positive, we can conclude that:
sin ∠ C = ∣ cos ∠ C ∣
All we have to do is solve that equation:
sin 2 ∠ C = cos 2 ∠ C tan 2 ∠ C = 1 tan ∠ C = ± 1 ∠ C = 4 π or ∠ C = 4 3 π
We see that both of these solutions work, so those are the possible values.
Thanks for the solution!! Cheers!!
I use the cosine rule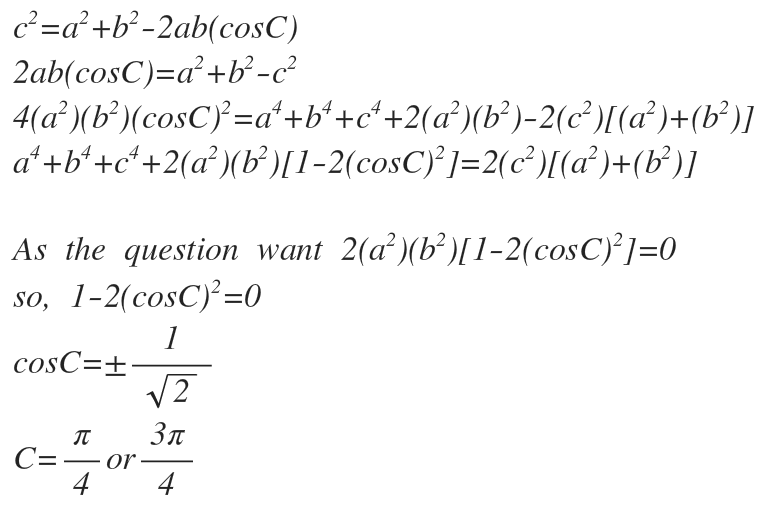 I think solve like this is easier.
I think solve like this is easier.