A Geometry Problem . T^3 Tilted, Turned And Twisted Maths
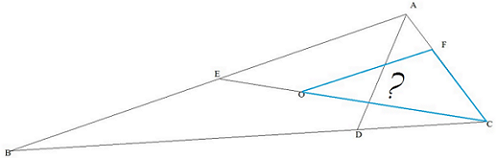
is a triangle in which is the bisector of angle such that . and . is the median on side of triangle . is the centroid of the triangle . Through a line is drawn. Find the area of triangle in .
Round your answer to 2 decimal places.
The answer is 25.66.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.

Draw AG perpendicular on line BC . ( Note : It will meet BC in the part DC and not in BD.)
Let AB = 3 x , AC = x ,
(by angle bisector theorem we know that bisector of any angle of a triangle divides the base side in the same ratio as the remaining sides .'. BD : CD= 3:1 Let BD = 3 y and DC = y
In right triangle AGD ,
=> A D A G =sin 60
=> 1 0 c m A G = 2 √ 3
=> AG = 2 1 0 √ 3 c m
=> AG = 5√3 cm
Also, A D D G = cos 60
=> 1 0 c m D G = 2 1
=> DG = 5 cm
In right triangle AGB,
AB^2 - BG^2 = AG^2 (by Pythagoras theorem )
=> (3 x )^2 - (BD + DG )^2 = (5√3)^2
=> 9 x ^2 - (3 y +5 )^2 = 75
=> 9 x ^2 - 9 y ^2 - 30 y - 25 = 75
=> 9 x ^2 - 9 y ^2 - 30 y =100 ------------------------------ eq n (1)
Similarly , in triangle AGC ,
AC^2 - GC^2 = AG^2 (by Pythagoras theorem )
=> x ^2 - (DC - DG )^2 = (5√3)^2
=> x ^2 - ( y - 5 )^2 = 75
=> x ^2 - y ^2 + 10 y - 25 = 75
=> x ^2 - y ^2 + 10 y = 100
=> 9 x ^2 - 9 y ^2+ 90 y = 900 ------------------------------------ eq n (2) (Multiplying both sides of eq n by 9)
Subtracting equation (1) from equation (2) , we get :
120 y = 800
=> y = 1 2 0 8 0 0
=> y = 3 2 0
.'. BC = BD + DC
= 3 y + y
= 4 y
= 4 * 3 2 0
= 4 * 3 2 0
= 3 8 0
.'. Area of △ ABC = 2 1 * AG * BC
= 2 1 * 5√3 cm * 3 8 0
= 3 2 0 0 √ 3 c m 2
'.' We know that median of a triangle divides a triangle into two triangles of equal area.
.'. Ar . △ ECA = 2 1 Area of △ ABC = 3 ∗ 2 2 0 0 √ 3 c m 2
= 3 1 0 0 √ 3 c m 2
Now , in △ ECA and △ OFC ,,
∠ C = ∠ C ( Common )
& ∠A = ∠ CFO ( '.' EA || OF .'. alt. int. ∠s are equal )
.'. △ ECA ~ △ OFC --(by AA similarity criterion)
.'. A r . △ O F C A r . △ E C A = O F 2 C O 2 ( In similar triangles ratio of area of triangles = ratio of .. square of corresponding sides of the triangle ) => A r . △ O F C A r . △ E C A = C O C E ^2 ------------ eq n (3)
We know that centroid divides median in ratio 2:1
.'. CO : OE = 2 : 1
=> OE: CO =1 : 2
=> C O O E + 1 = 2 1 +1
. => C O O E + C O = 2 3
=> C O C E = 2 3
Putting CE/CO = 3/2 in equation 3 , we gets :
=> A r . △ O F C A r . △ E C A = 2 3 ^2
=> A r . △ O F C A r . △ E C A = 4 9
=> A r . △ O F C ( 1 0 0 √ 3 / 3 ) c m 2 = 4 9 ('.' Area of △ ECA = 3 1 0 0 √ 3 c m 2
=> Ar. △ OFC = 3 ∗ 9 1 0 0 √ 3 ∗ 4 c m 2
= 25.660
* This question has been TILTED using GEOMETRY, TURNED from its original path using ALGEBRA and finally TWISTED . using TRIGONOMETRY . *