Is logarithms required?
If 2 x = 4 y = 8 z and x y z = 2 8 8 , with 2 x 1 + 4 y 1 + 8 z 1 = n m for coprime positive integers m and n , find m + n .
The answer is 107.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Since 2 x = 4 y = 8 z , y = lo g 2 ( 4 ) x = 2 x , z = lo g 2 ( 8 ) x = 3 x and since x y z = 2 8 8 , substituting the above equations and solving for x gives x = 3 1 7 2 8 = 1 2 . Finally, 2 4 1 + 2 4 1 + 3 2 1 = 9 6 1 1 1 1 + 9 6 = 1 0 7
Oh! I didn't see that it was 1/(2x) + 1/(4y) + 1/(8z) ! I thought I was supposed to figure out what m and n were after summing (12/2 + 6/4 + 4/8). I didn't think that was possible, especially since m and n were not necessarily prime. I wish this problem had been easier to read. :p
By making the bases as same we get x=2y=3z
let x=2y=3z=k
x=k ,y=k/2,z=k/3
sub the above values in xyz=288
k.k/2.k/3=288
k^3/6=288
k^3=1728
k=12 and not -12 because xyz=288 and not -288
x=12,y=6,z=4
sub the above values in 1/2x+1/4y+1/8z=m/n
and u will get the answer as m/n =11/96
since 11/96 is coprime m+n =107
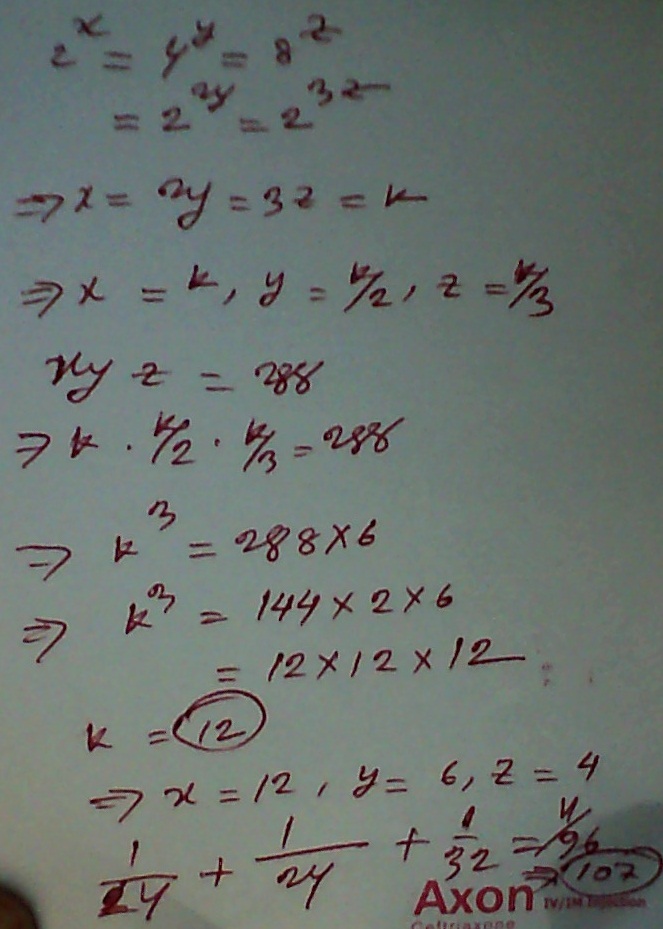
Simple,
Easily can be seen that
x = 2 y = 3 z
Therefore,
6 x y z = x 3
Therefore
x = 1 2
The rest is too easy to explain.