Just write the word!
On how many different ways you can "write" the word "SODALG" starting with the red letter S and moving afterwards on to the neighboring letter.
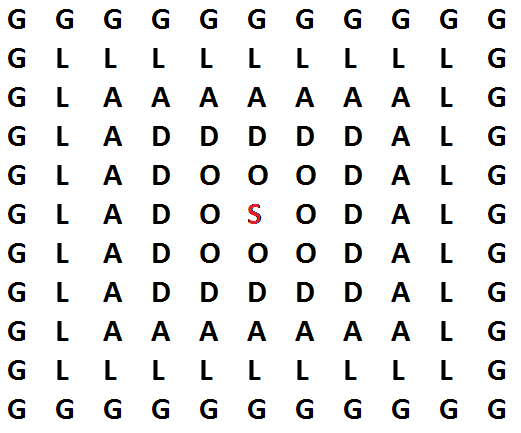
Details and assumptions:
A "Neighboring letter" is either down, up, right, left, up-left, up-right, down-left or down-right from the temporary letter. For example, if we start with S and word "SO" is required, there are 8 ways to "write" it.
If you have questions relevant to this problem, you can always ask here .
The answer is 968.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Touché. My response was 4 only because I thought it was more of a riddle. And we read left to right making the opposing side irrelevant.
I don't get why a 2 = 8 , even though there are clearly nine ways to 'write' 'SO'.
I solved it my self assuming a 2 = 9 and got it right...
Log in to reply
How did you get a 2 = 9 ? Aren't there only 8 'O's and 1 'S'? If you got it right then maybe you defined it differently?
Log in to reply
How the heck did I solve it😂😂😂😂? Those o's and the s were on a 3x3 square and 3x3 square makes me instantly think 9. Maybe that's why I thought it was nine but how did I solve it with that assumption😅 I'm so confused😂
I made the same observations, but handled it differently afterwards (see the non-recursive general formula in my solution below).
Has anyone not noticed that "SOLDAG" backwards is "GLADOS"?
Anyways, we consides the top quarter of the figure first, i.e. how many ways to get to the G's to the top. Starting from the S, you can move 5 times upward either in a north-east, north or north-west direction so 3 choices and 5 moves, giving us 3 5 = 2 4 3 ways to get to the top layer of G's.
We multiply this number by 4 to obtain the number of ways to get to all the G's on the sides. However, this double-counts the number of ways to get to the corners. Since there is exactly 1 way to get to any corner G, and there are 4 such corners, we subtract the result by 4 .
Our answer is then ( 4 ) ( 2 4 3 ) − 4 = 9 6 8 .
I'm glad that somebody noticed :)
Loved te answer. But SOLDAG backwards is not GLADOS. Its GADLOS. U see? Kind like GETTLOSS. Just a joke though
Log in to reply
Ahahahaha. Now GETLOSS XD
joke joke
I don't know what GLADOS is, though. I just heard of (it?) from a game
Log in to reply
Yes. Now that u mentioned it. I think I have heard it in some game sometime. Anyway, congratulation for your answer. I dont do Math. Im a philosphy student. But I can recognize the beauty of your answer
I made the same observations as Shaun Leong, but took a different path afterwards (3 ways everywhere and 2 additional ways at the 4 corners (each layer).
I ended up with the following closed (non-recursive) formula:
8 × 3 4 + 4 × 2 × 3 3 + 4 × 2 × 3 2 + 4 × 2 × 3 + 4 × 2 = 9 6 8
If we also find, that 4 × 2 = 8 and therefore, we are dealing with a geometric series, we can get a general formula for n letters:
8 × 3 − 1 3 n − 1 − 1 = 4 × ( 3 n − 1 − 1 ) = 4 × 3 n − 1 − 4
And this is the general form of the formula, what Manuel Kahayon used, as for n = 6 ("SODALG" has 6 letters), we get
4 × 3 5 − 4 = 9 6 8
Let a n be the number of ways to get to the n -th "layer". We know a 2 = 8 and we want to find a 6 .
We make the following observations about a n + 1 :
Out of a n ways, 4 of them end at corners. From each of these corners, there are 5 neighbouring letters.
The rest of the a n − 4 ways have 3 neighbouring letters.
Hence a n + 1 = 3 ( a n − 4 ) + 4 ∗ 5 ⇒ a n + 1 = 3 a n + 8
Given a 2 = 8 , we get a 6 = 9 6 8