This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Watch my video for the solution to this problem -> http://youtu.be/Oh-b3DT_xow
For the solution in text: ---Part 1. - Finding the remainder of 2 1 0 0 --- We can rewrite any number as a + b, where 'a' is divisible by 7 and 'b' is a remainder. When we square this number, we will get ( a + b ) 2 = a 2 + 2 a b + b 2 , so the remainder will also be squared (the first two terms are divisible by 7 since they contain 'a'). The remainder when 2 3 is divided by 7 is 1, so when 8 is taken to any power of a power of 2 (as in 8 2 n ) and divided by 7, the remainder will still be 1. When substituting n with 5, you get 2 9 6 . To get to 2 1 0 0 from 2 9 6 , one must multiply by 2 4 (16), in turn multiplying the remainder (1) by 16. Having a remainder of 16 is mathematically equivalent to having a remainder of 2 since 16 is still divisible by 7. The remainder when 2 1 0 0 is divided by 7 is therefore 2.
---Part 2. The remainder of 4 1 0 0 --- The remainder when 2 1 0 0 + 3 1 0 0 + 4 1 0 0 + 5 1 0 0 is divided by 7 is equivalent to the sum of the remainders when each of the 4 terms are divided by 7. We already know the remainder of 7 2 1 0 0 = 2 . From exponent laws we know 4 1 0 0 = 2 2 0 0 = ( 2 1 0 0 ) 2 , and as stated in part 1 of this solution, we showed how squaring a number will result in it's remainder becoming squared too. Therefore the remainder when 2 2 0 0 is divided by 7 is 2 2 = 4 .
---Part 3. The remainder of 3 1 0 0 and 5 1 0 0 --- Note that 5 can be rewritten as 7-2, so 5 1 0 0 = ( 7 − 2 ) 1 0 0 . The binomial expansion looks something like ( 7 − 2 ) 1 0 0 = 7 1 0 0 − 7 9 9 × 2 1 + 7 9 8 × 2 2 − . . . . + 7 2 × 2 9 8 − 7 1 × 2 9 9 + 2 1 0 0 . As you can see all terms except the last one contain at least one 7 and are therefore divisible by 7. Since only the term 2 1 0 0 is not divisible by 7 in the expansion, the remainder of 5 1 0 0 is equivalent to that of 2 1 0 0 , which is equal to 2. We can do the same thing for 3 1 0 0 , as 3 can be rewritten as 7-4 and ( 7 − 4 ) 1 0 0 = 7 1 0 0 − 7 9 9 × 4 1 + . . . . − 7 1 × 4 9 9 + 4 1 0 0 . Again the only term not divisible by 7 is 4 1 0 0 , which means the remainder of 3 1 0 0 is the same as that of 4 1 0 0 which is equal to 4.
Adding all the remainders of 2 1 0 0 + 3 1 0 0 + 4 1 0 0 + 5 1 0 0 = 2 + 4 + 4 + 2 = 1 2 . Having a remainder of 12 is equivalent to having a remainder of 5 since 12 is still divisible by 7.
Therefore, the remainder when 2 1 0 0 + 3 1 0 0 + 4 1 0 0 + 5 1 0 0 is divided by 7 = 5
pls expand and tell what is modulo I would be very grateful to you.
I'm not exactly sure, but it's a way of talking about remainders. For example, 12 modulo 7 is congruent to 5 modulo 7, since 12/7 and 5/7 have the same remainder. I'm sure the people who wrote about modulo could expand on it.
2+3+4+5=14 modulo 7 =0 2^2 + 3^2 + 4^2 + 5^2= 54 modulo 7 =5 generalizing 2^n + 3^n + 4^n + 5^n =x modulo 7 = 0 or 5 when n is odd or even...
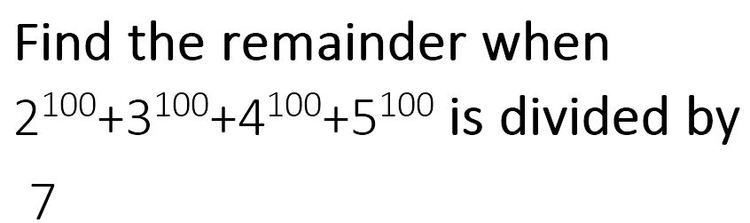
By congruency, we know that
2 1 0 0 is congruent to 2 modulo 7
3 1 0 0 is congruent to 4 modulo 7
2 2 0 0 is congruent to 4 modulo 7
5 1 0 0 is congruent to 2 modulo 7
Adding all, we get, req. is congruent to 5 modulo 7. Hence, 5