Keep Off The Grass

Applying the pythagorean theorem , we get

$(AD)^2=12^2+9^2=144+81=225$

$AD=\sqrt{225}=$ $\boxed{15}$

Relevant wiki: Pythagorean Theorem

Let's call the lower left corner (on the same side as $D$ and $C$ ) $E$ , $AE$ is parallel to $BC$ .

Now, we have a right angled triangle: $AED$ , with side lengths:
$AE = BC = 12$
$DE = AB + CD = 3 + 6 = 9$

By applying Pythagoras' theorem:
$AE^2 + DE^2 = AD^2$

$AD = \sqrt {9^2 + 12^2} = \sqrt {81 + 144} = \sqrt {225} = \boxed {15}$ .

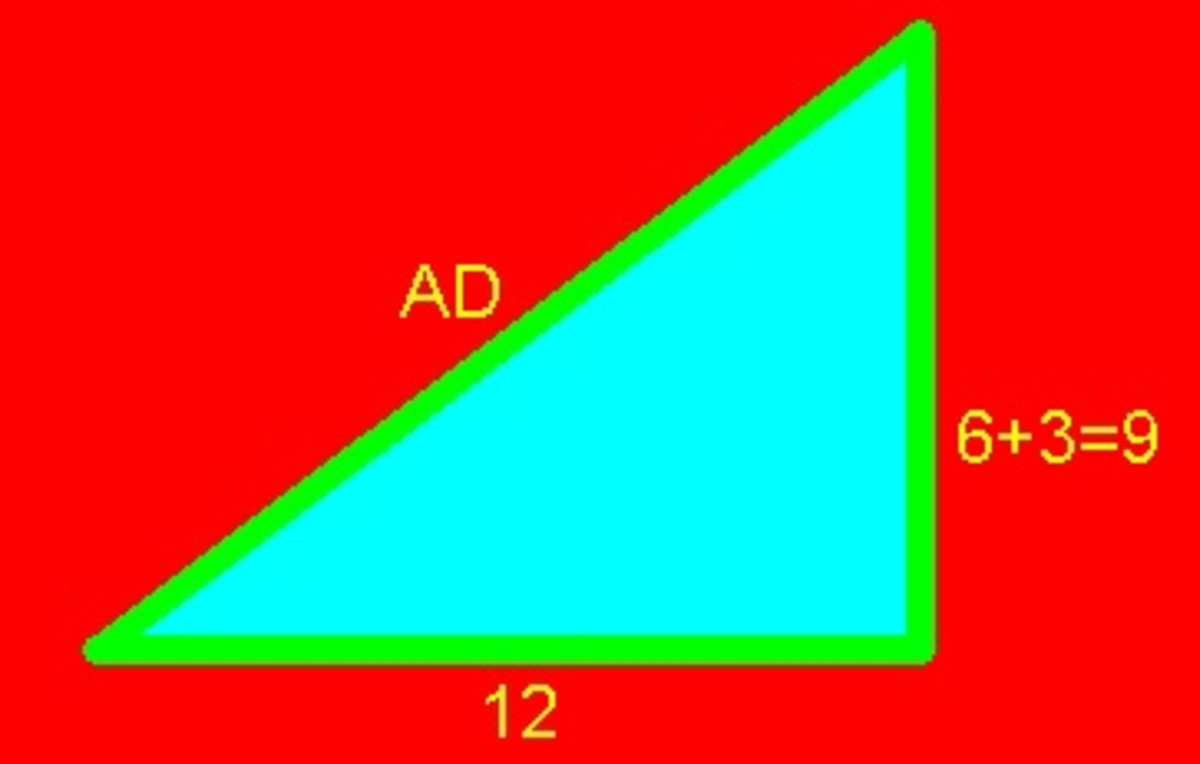By Pythagorean Theorem, we have

$(AD)^2=12^2+9^2$

$(AD)^2=144+81$

$(AD)^2=225$

$AD=\sqrt{225}=$ $\large\color{#3D99F6}\boxed{15}$ $\color{#69047E}\boxed{\text{answer}}$

The man behind the pythagorean theorem :

Pythagoras of Samos (US /pɪˈθæɡərəs/;[1] UK /paɪˈθæɡərəs/; Greek: Πυθαγόρας ὁ Σάμιος Pythagóras ho Sámios "Pythagoras the Samian", or simply Πυθαγόρας; Πυθαγόρης in Ionian Greek; c. 570 – c. 495 BC) was an Ionian Greek philosopher, mathematician, and putative founder of the Pythagoreanism movement. He is often revered as a great mathematician and scientist and is best known for the Pythagorean theorem which bears his name.

Legend and obfuscation cloud his work, so it is uncertain whether he truly contributed much to mathematics or natural philosophy. Many of the accomplishments credited to Pythagoras may actually have been accomplishments of his colleagues or successors. Some accounts mention that the philosophy associated with Pythagoras was related to mathematics and that numbers were important. It was said that he was the first man to call himself a philosopher, or lover of wisdom, and Pythagorean ideas exercised a marked influence on Plato, and through him, all of Western philosophy.

Relevant wiki: Pythagorean Theorem

Suppose AD and BC intersects at point E. We can see that the intersected angles of ∠AEB and ∠CED are equal.

Also, since triangles AEB and CED are right triangles and have the same intersected angles, making the other complementary angles equal, these two triangles are similar.

Now since the ratio of AB : CD = 3 : 6 = 1 : 2, the ratio of BE : EC also equals 1 : 2.

Suppose BE = x for some number x.

Then x + 2x = 12; x = 4.

As a result, by using Pythagorean theorem, AE2 = AB2 + BE2 = 32 + 42 = 25.

Thus, AE = 5.

By using the same ratio, ED = 10.

Therefore, AD = AE + ED = 15.

If you put the two measurements (6 and 3) to any one lf the width of rectangle . Then a right triangle form with the legs 9 and 12. So we can apply the pythagorean theorem .

$(AD)^{2} = 9^{2}+12^{2}=81+144=225$
$(AD^{2} = 225 = 15^{2}$

So ultimately $AD = \boxed{15}$

[We can put the muasurements into any width of the rectangle because the measurements are the width of the two divided rectangle whose width are seperately conncetde to the width of the main rectangle]

This can be simplified it is a Pythagorean triple like a 3, 4, 5 triangle virtually no math involved