Keep your distance
 Let
Δ
A
B
C
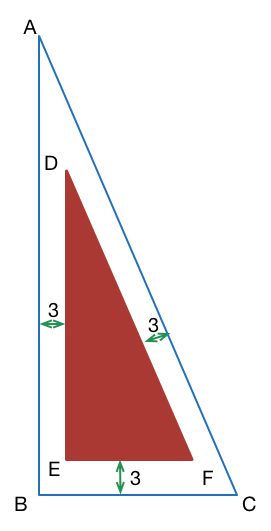
have integer side lengths and be right-angled at
B
. Now suppose
Δ
D
E
F
is located within
Δ
A
B
C
with the same orientation, such that its sides are parallel to the corresponding sides of
Δ
A
B
C
and the distance between the corresponding parallel sides is
3
.
Let
Δ
A
B
C
have integer side lengths and be right-angled at
B
. Now suppose
Δ
D
E
F
is located within
Δ
A
B
C
with the same orientation, such that its sides are parallel to the corresponding sides of
Δ
A
B
C
and the distance between the corresponding parallel sides is
3
.
If the area of Δ A B C is 4 times that of Δ D E F then there are n possible triangles Δ A B C independent of orientation. If S is the sum of the lengths of the hypotenuses of these n triangles, then find n + S .
The answer is 273.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Amazing problem. Thanks Sir!
Impressive. I totally failed at attacking this problem.

(
1
2
,
3
7
,
3
5
)
:
−
a
=
6
∗
(
1
+
3
5
3
7
+
1
2
)
=
5
7
2
.
a
/
x
N
o
t
a
n
i
n
t
e
g
e
r
.
N
o
s
o
l
u
t
i
o
n
.
(
9
,
4
1
,
4
0
)
:
−
a
=
6
∗
(
1
+
4
0
4
1
+
9
)
=
2
2
7
.
a
/
x
N
o
t
a
n
i
n
t
e
g
e
r
.
N
o
s
o
l
u
t
i
o
n
.
(
2
8
,
5
3
,
4
5
)
:
−
a
=
6
∗
(
1
+
4
5
5
3
+
2
8
)
=
5
5
4
.
a
/
x
N
o
t
a
n
i
n
t
e
g
e
r
.
N
o
s
o
l
u
t
i
o
n
.
(
1
1
,
6
1
,
6
0
)
:
−
a
=
6
∗
(
1
+
6
0
6
1
+
1
1
)
=
5
6
6
.
a
/
x
N
o
t
a
n
i
n
t
e
g
e
r
.
N
o
s
o
l
u
t
i
o
n
.
(
1
6
,
6
5
,
6
3
)
:
−
a
=
6
∗
(
1
+
6
3
6
5
+
1
6
=
7
5
4
.
a
/
x
N
o
t
a
n
i
n
t
e
g
e
r
.
N
o
s
o
l
u
t
i
o
n
.
(
3
3
,
6
5
,
5
6
)
:
−
a
=
6
∗
(
1
+
5
6
6
5
+
3
3
)
=
2
2
1
.
a
/
x
N
o
t
a
n
i
n
t
e
g
e
r
.
N
o
s
o
l
u
t
i
o
n
.
(
4
8
,
7
3
,
5
5
)
:
−
a
=
6
∗
(
1
+
5
5
7
3
+
4
8
)
=
5
1
0
8
.
a
/
x
N
o
t
a
n
i
n
t
e
g
e
r
.
N
o
s
o
l
u
t
i
o
n
.
(
3
6
,
8
5
,
7
7
)
:
−
a
=
6
∗
(
1
+
7
7
8
5
+
3
6
)
=
7
1
0
8
.
a
/
x
N
o
t
a
n
i
n
t
e
g
e
r
.
N
o
s
o
l
u
t
i
o
n
.
(
3
9
,
8
9
,
8
0
)
:
−
a
=
6
∗
(
1
+
8
0
8
9
+
3
9
)
=
5
7
8
a
/
x
N
o
t
a
n
i
n
t
e
g
e
r
.
N
o
s
o
l
u
t
i
o
n
.
(
6
5
,
9
7
,
7
2
)
:
−
a
=
6
∗
(
1
+
7
2
9
7
+
6
5
)
=
2
3
9
a
/
x
N
o
t
a
n
i
n
t
e
g
e
r
.
N
o
s
o
l
u
t
i
o
n
.
W
e
c
a
n
s
e
e
t
h
a
t
n
o
t
o
n
l
y
a
/
x
i
s
n
o
t
a
n
i
n
t
e
g
e
r
b
u
t
i
t
i
s
a
l
s
o
l
e
s
s
t
h
a
n
1
.
s
o
d
i
d
n
o
t
c
h
e
c
k
f
u
r
t
h
e
r
.
A
n
y
b
e
t
t
e
r
e
x
p
l
a
n
a
t
i
o
n
w
i
l
l
b
e
a
p
p
r
e
c
i
a
t
e
d
.
B
e
t
t
e
r
S
o
l
u
t
i
o
n
A
N
Y
P
Y
T
H
A
G
O
R
E
A
N
R
I
G
H
T
T
R
I
A
N
G
L
E
W
I
T
H
I
N
R
A
D
I
U
S
=
6
I
S
T
H
E
S
O
L
U
T
I
O
N

i 6 m u s t b e a n i n t e g e r . ∴ i m u s t b e a f a c t o r o f 6 ( 1 2 , 3 7 , 3 5 ) : − i = 5 . i 6 N o t a f a c t o r o f 6 . N o s o l u t i o n . ( 9 , 4 1 , 4 0 ) : − i = 4 . i 6 N o t a f a c t o r o f 6 . N o s o l u t i o n . ( 2 8 , 5 3 , 4 5 ) : − i = 1 0 . i 6 N o t a f a c t o r o f 6 . N o s o l u t i o n ( 1 1 , 6 1 , 6 0 ) : − i = 5 . i 6 N o t a f a c t o r o f 6 . N o s o l u t i o n ( 1 6 , 6 5 , 6 3 ) : − i = 3 . 5 . i 6 N o t a f a c t o r o f 6 . N o s o l u t i o n ( 3 3 , 6 5 , 5 6 ) : − i = 1 2 . i 6 N o t a f a c t o r o f 6 . N o s o l u t i o n ( 4 8 , 7 3 , 5 5 ) : − i = 1 5 . i 6 N o t a f a c t o r o f 6 . N o s o l u t i o n ( 3 6 , 8 5 , 7 7 ) : − i = 1 4 . i 6 N o t a f a c t o r o f 6 . N o s o l u t i o n ( 3 9 , 8 9 , 8 0 ) : − i = 1 5 . i 6 N o t a f a c t o r o f 6 . N o s o l u t i o n ( 6 5 , 9 7 , 7 2 ) : − i = 2 0 . i 6 N o t a f a c t o r o f 6 . N o s o l u t i o n I n c i d e n t a l l y i n a r t i c l e s o n r i g h t t r i a n g l e s o n e c a n s e e t h a t t h e r e a r e o n l y S I X t r i a n g l e s w i t h i n r a d i u s r = 6 .
W e s a w t h a t t h e r e q u i r e d t r i a n g l e s h o u l d b e P y t h a g o r e a n r i g h t t r i a n g l e w i t h i n r a d i u s = 6 . F r o m t h e w e b w e k n o w t h a t t h e r e a r e s i x s u c h t r i a n g l e s a n d t h e i r s i d e s a r e a l s o g i v e n . W e a d d t h e l e n g t h s o f t h e i r h y p o t e n u s e s .
If we set up a coordinate system so that the right angle of the triangle is at the origin and two vertices are at ( a , 0 ) and ( 0 , b ) , then the equation of the hypotenuse of the smaller triangle is b x + a y = a b − 3 a 2 + b 2 = a b − 3 c and so the coordinates of the vertices of the smaller triangle are ( 3 , 3 ) , ( 3 , a a b − 3 b − 3 c ) and ( b a b − 3 a − 3 c , 3 ) , so the non-hypotenuse sides of the smaller triangle are p = b 1 ( a b − 3 a − 3 b − 3 c ) q = a 1 ( a b − 3 a − 3 b − 3 c ) The area condition that 2 1 a b = 4 × 2 1 p q now becomes a 2 b 2 = 4 ( a b − 3 a − 3 b − 3 c ) 2 , and hence 3 ( a b − 2 a − 2 b − 2 c ) ( a b − 6 a − 6 b − 6 c ) = 0 We cannot have a b = 2 a + 2 b + 2 c , since that would force p , q to be negative. Thus we deduce that a b = 6 a + 6 b + 6 c which tells us that p = 2 1 a and q = 2 1 b . Since ( a , b , c ) is a Pythagorean triad, and we don't care about its orientation, we can find positive integers d , u , v such that a = d ( u 2 − v 2 ) , b = 2 d u v , c = d ( u 2 + v 2 ) . The above condition now becomes d v ( u − v ) = 6 There are 9 different solutions for d , u , v , and these produce exactly 6 different Pythagorean triads ( a , b , c ) , namely ( 1 3 , 8 4 , 8 5 ) , ( 1 4 , 4 8 , 5 0 ) , ( 1 5 , 3 6 , 3 9 ) , ( 1 6 , 3 0 , 3 4 ) , ( 1 8 , 2 4 , 3 0 ) , ( 2 0 , 2 1 , 2 9 ) . This makes the answer to the question 2 7 3 .
Let D E ∣ ∣ A B , E F ∣ ∣ B C and D F ∣ ∣ A C . Also let sides A B , B C , A C have respective lengths a , b , c . Since the area of Δ A B C is 4 times that of Δ D E F we then have that D E = 2 a , E F = 2 b and D F = 2 c .
Now break Δ A B C into trapezoids A D E B , B E F C and A D F C , as well as Δ D E F . Adding up the areas of these latter four regions and equating the sum to the area of the larger triangle, we have that
3 ( 4 3 a ) + 3 ( 4 3 b ) + 3 ( 4 3 c ) + 8 a b = 2 a b
⟹ 6 a + 6 b + 6 c = a b ⟹ a b − 6 a − 6 b = 6 c = 6 a 2 + b 2
⟹ a 2 b 2 + 3 6 a 2 + 3 6 b 2 − 1 2 a b 2 − 1 2 a 2 b + 7 2 a b = 3 6 a 2 + 3 6 b 2
⟹ a b ( a b − 1 2 a − 1 2 b + 7 2 ) = 0 ⟹ b ( a − 1 2 ) = 1 2 a − 7 2
⟹ b = 1 2 + a − 1 2 7 2 .
Since b must be an integer, we must have a − 1 2 as a (positive) factor of 7 2 . The possible values of a are then 1 3 , 1 4 , 1 5 , 1 6 , 1 8 , 2 0 , 2 1 , 2 4 , 3 0 , 3 6 , 4 8 , 8 4 .
Upon calculating corresponding values for b and c , we find that there are 6 possible triangles independent of orientation, namely
( 1 3 , 8 4 , 8 5 ) , ( 1 4 , 4 8 , 5 0 ) , ( 1 5 , 3 6 , 3 9 ) , ( 1 6 , 3 0 , 3 4 ) , ( 1 8 , 2 4 , 3 0 ) , ( 2 0 , 2 1 , 2 9 ) .
The desired sum is then 6 + 8 5 + 5 0 + 3 9 + 3 4 + 3 0 + 2 9 = 2 7 3 .