Keeping Things in Perspective
You are looking down at 4 unit cubes on a level surface. From this point of view, cube O is in the center, cube P is placed 3 units left and 2 units up from cube O , cube Q is placed 1 unit right and 3 units down from cube O , and cube R is placed 5 units right and 1 unit up from cube O .
You draw these cubes to scale using one-point perspective , with the vanishing point centered directly underneath cube O , as pictured below.
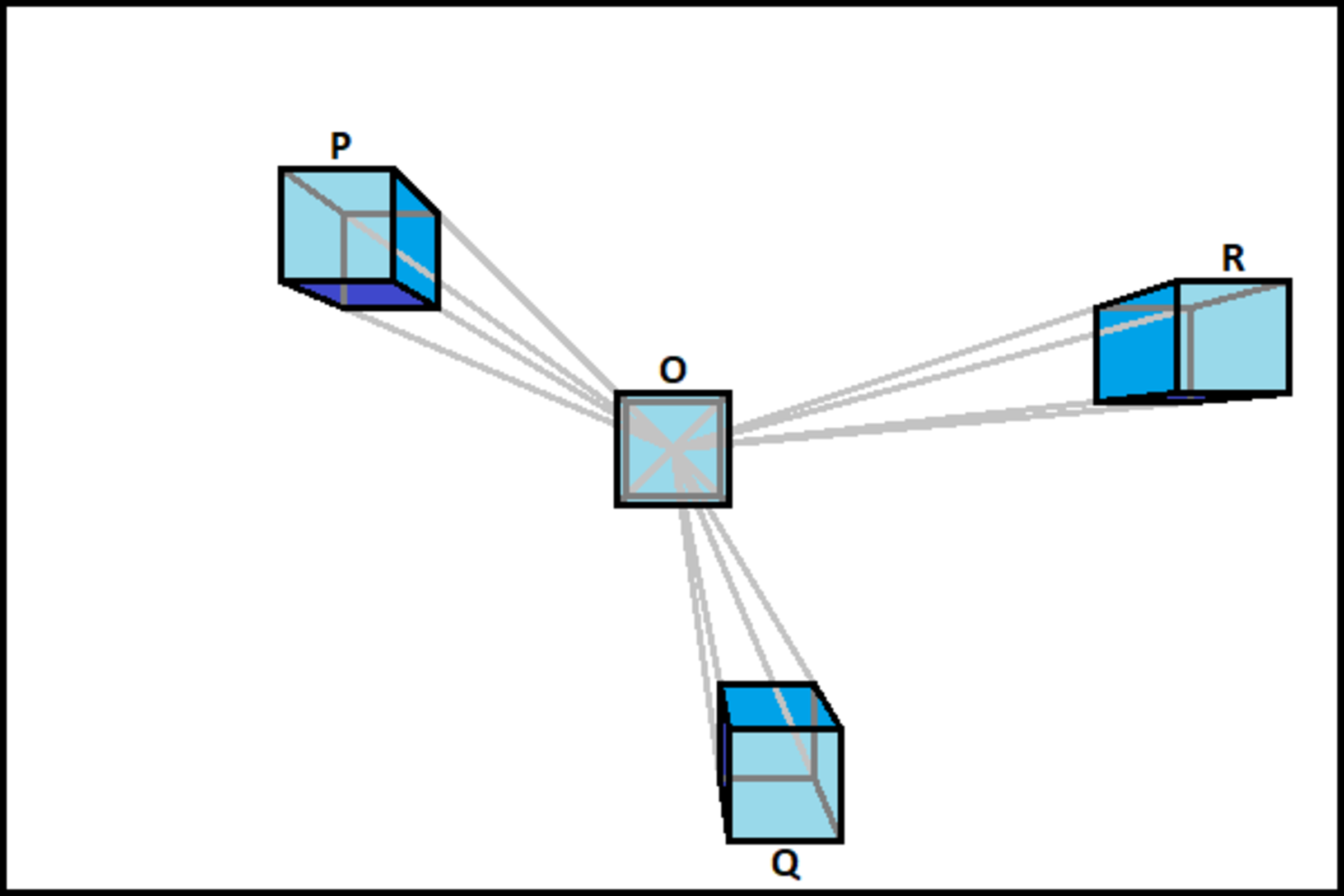
You then create a silhouette of each cube by coloring inside its drawn outline. As a result, the silhouette of cube O is a square, and the silhouettes of cubes P , Q , and R are hexagons, as pictured below.
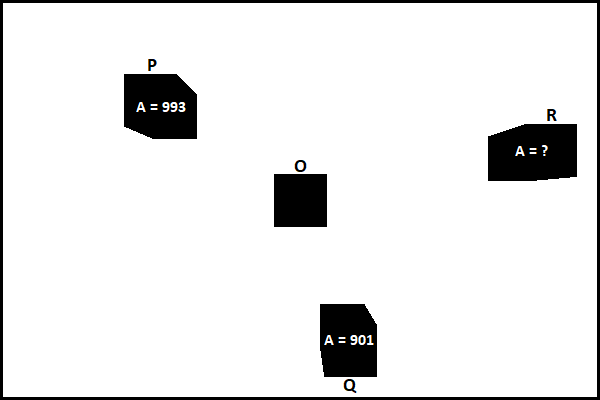
If the area of the hexagon formed by cube P is 9 9 3 and the area of the hexagon formed by cube Q is 9 0 1 , what is the area of the hexagon formed by cube R ?
The answer is 1085.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Can you show how you derived those equations?
Log in to reply
yeah I'll get to that, it's tedious... the point of those equations is to show that the answer is an exact integer 1085
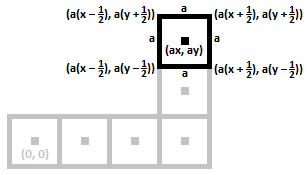
Since all the cubes are on a level surface, the sides of the bottom and top faces of each drawn cube stays constant, but the difference of where they are drawn in relation to each other is proportional to how far away from the origin the cube is. The center of the top square with a fixed side length of a in the first quadrant that is x units to the right and y units up from the origin would be drawn at ( a x , a y ) and vertices at ( a ( x ± 2 1 ) , a ( y ± 2 1 ) ) .
Likewise, the bottom square with a fixed side length of b would have vertices at ( b ( x ± 2 1 ) , b ( y ± 2 1 ) ) .
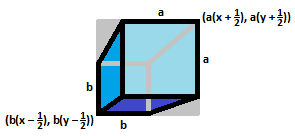
This means that the area of hexagonal silhouette of the perspective cube is the difference between the area of the rectangle with sides c = a ( x + 2 1 ) − b ( x − 2 1 ) and d = a ( y + 2 1 ) − b ( y − 2 1 ) and the areas of the two opposite triangles, one with sides c − a and d − b , and the other with sides c − b and d − a . In other words, the area of the hexagon is A = c d − 2 1 ( c − a ) ( d − b ) − 2 1 ( c − b ) ( d − a ) , and letting p = 2 1 ( a 2 − b 2 ) and q = 2 1 ( a 2 + b 2 ) this simplifies to A = p ( x + y ) + q .
A similar argument can be made for each quadrant to give the general formula of A = p d + q , where d = ∣ x ∣ + ∣ y ∣ . Surprisingly, this means that the hexagonal area is a linear function based on its taxicab distance from the origin.
In this problem, hexagon P has an area of 9 9 3 with a taxicab distance of d P = ∣ − 3 ∣ + ∣ 2 ∣ = 5 from the origin, and hexagon Q has an area of 9 0 1 with a taxicab distance of d Q = ∣ 1 ∣ + ∣ − 3 ∣ = 4 from the origin. Using the above equation, we get 9 9 3 = 5 p + q and 9 0 1 = 4 p + q , which solves to p = 9 2 and q = 5 3 3 . Therefore, hexagon R , with a taxicab distance of d R = ∣ 5 ∣ + ∣ 1 ∣ = 6 from the origin, has an area of A = 6 p + q = 6 ⋅ 9 2 + 5 3 3 = 1 0 8 5 .
Let d be the distance from the observer to the face of the cube at the origin. Then, if
2 d 2 + 1 0 d + 5 2 d 2 + 1 2 d + 6 = 9 0 1 9 9 3
then
2 d 2 + 1 2 d + 6 2 d 2 + 1 4 d + 7 = 9 9 3 1 0 8 5
and so the answer is 1 0 8 5
Let the origin ( 0 , 0 , 0 ) be at the center of cube O and ( 0 , 0 , − d − 2 1 ) be the coordinate of the POV. Then the coordinates of all the vertices of cubes P , Q , R relative to the POV are found by adding ( ± 2 1 , ± 2 1 , ± 2 1 ) to ( − 3 , 2 , d + 2 1 ) , ( 1 , − 2 , d + 2 1 ) , ( 5 , 1 , d + 2 1 ) respectively. Thus, if we project the vertices onto the plane ( 0 , 0 , − 2 1 ) , then the adjustment factor between the vertices at ( x , y , − 2 1 ) and ( x , y , + 2 1 ) is d d + 1 . So, for example, the coordinates of the projected irregular hexagon silhouette of cube P are
( − 2 5 , 2 5 )
( − 2 5 , 2 3 )
( − 2 7 , 2 3 )
( − 2 d 7 ( d + 1 ) , 2 d 3 ( d + 1 ) )
( − 2 d 7 ( d + 1 ) , 2 d 5 ( d + 1 ) )
( − 2 d 5 ( d + 1 ) , 2 d 5 ( d + 1 ) )
which has the area of
2 d 2 2 d 2 + 1 2 d + 6
We do likewise for cubes Q and P , with areas
2 d 2 2 d 2 + 1 0 d + 6
2 d 2 2 d 2 + 1 4 d + 7
respectively
In determining the area the silhouette of cube R , we only need to consider relative ratios of the areas of the silhouette at any plane of projection, so we can drop the term 2 d 2 .
See Shoelace formula for computing areas of irregular polygons given the coorindates of its vertices.