Calcudoku Puzzle - 5 x 5
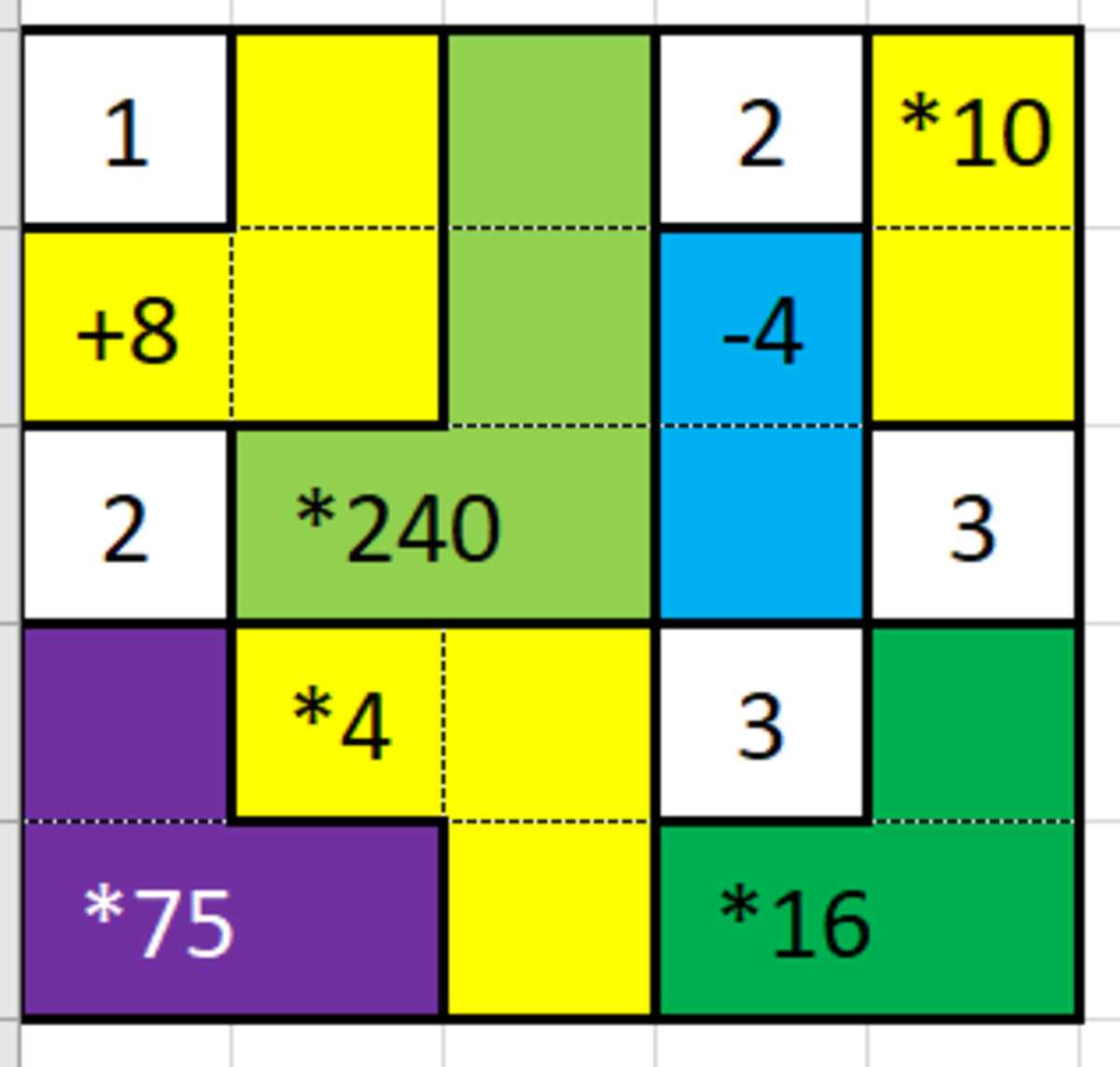
The following is a Calcudoku puzzle. Each of the "cages" is to be filled with a sequence of numbers (not necessarily distinct), such that the operation specified on the cage is satisfied, and such that after filling all the cages, each row and each column contains all the digits from to . The single white squares are already supplied with given digits. Solve the puzzle and report the sequence of digits of the second row.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The first column already has {1,2} and needs {3,4,5}. However, 4 does not divide 75. Thus 4 is the first number in the second row.
Moving one step to the right, we a yellow shape with three numbers summing to 8, of which one is 4. Since the other two numbers are both in the second column, they must be 1 and 2. We already have a '1' in the first row, thus the '1' in this shape must be in the second row, and the '2' in the first row.
The yellow cage on the far right has two numbers that multiply to 10, i.e. '2' and '5'. Since there is already a '2' in the first row, in this cage the '5' is on the top and the '2' is in the second row.
So far we have 41**2. The only choices are 41352 and 41532. We still need to place the '3' and the '5'. The blue cage has two numbers that differ by 4. Thus the '5' must be in this cage and the '3' in the other spot, giving us a sequence of 41352.