Kidding me?
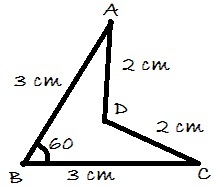
In the given figure, A B = 3 cm , B C = 3 cm , C D = 2 cm , A D = 2 cm . ∠ A B C = 6 0 ∘ . Find the area of the quadrilateral A B C D .
No trigonometry to be used.
Round off your answer correct to 2 decimal places.
Find your answer in sq cm units.
The answer is 1.91.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
its a relative easy problem i wonder why you put it level 4
Log in to reply
Well, I didn't put it on Level 4. @Brilliant Mathematics did.
Log in to reply
We do not manually change the levels. If more people can't solve this problem, then the level of this problem will naturally increase.
I've changed it back to level 3.
Clearly Isosceles triangle ABC with vertex angle 60 is equilateral. So AC=3. Altitude 0f ABC from B= 3 2 3 . I n i s o s c e l e s Δ A D C , a l t i t u d e f r o m D = A D 2 − ( 2 A C ) 2 = 2 7 . ∴ r e q u i r e d a r e a = 2 1 ∗ 3 ∗ ( 3 2 3 − 2 7 ) = 1 . 9 1 2 8
Join AC.
Now, In tr. ABC, AB = BC = 3 cm Hence angle BAC = angle BCA
Clearly, using angle sum property of triangles,
angle BAC = angle BCA = angle ABC = 60 degrees Clearly, tr. ABC is an equilateral triangle
Then, AB=BC=AC=3 cm
Now, area(quad. ABCD) = area(tr. ABC) - area(tr. ADC) = [rt(3)/4]3^2 - (3/2) rt[2^2 - (3^2)/4]
Simpilifying the above expression using rt(3) = 1.732 and any other irrational number upto 3 decimal places (we have to round it off correct to 2 decimal places), we come up to:
(15.588 - 7.937)/4 = 7.651/4 = 1.91275
Rounding it off correct to 2 decimal places, we get 1.91 as the final answer