Kinematics is fun!!!
Thomas throws a stone verticaly upward with velocity 5 0 m / s . John, who is standing 2 7 8 m above him, throws a stone downward with velocity 3 m / s , two second after the first stone being thrown. Find the height (in meters) of the point where those stones will meet in the air.
Assumes :
-
There are no air resistance
-
g = 1 0 m / s 2
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
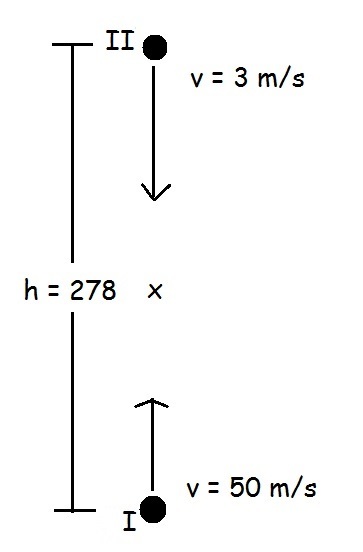
Let's say the stone being thrown upward as I and the downward one as I I . Those stones will meet in the air at the same time, let's call it t .
Assume the x as the point where stones meet, the distances the I stone had been travelled to x as S I , and the distances the I I stone had been travelled to x as S I I .
It will appears that S I + S I I = h
S I = v I . t I − 2 1 g t I 2 .
But be carefull, the I I stone being thrown 2 second after the I stone. That means the I stones travelled 2 seconds longer than the I I stone, or : t I = t + 2 . Then :
S I = 5 0 ( t + 2 ) − 2 1 1 0 ( t + 2 ) 2
S I = 3 0 t − 5 t 2 + 8 0
For the I I stone, the time is the same, t I I = t .
S I I = v I I t + 2 1 g t 2
S I I = 3 t + 2 1 1 0 t 2
S I I = 3 t + 5 t 2
Back to the main equation :
h = S I + S 2
2 7 8 = ( 3 0 t − 5 t 2 + 8 0 ) + ( 3 t + 5 t 2 )
1 9 8 = 3 3 t = > t = 6
The height of the point x will be the same as S I
x = S I = 3 0 t − 5 t 2 + 8 0
x = 3 0 . 6 − 5 . 6 2 + 8 0 = 8 0 m
Your solution is good but you can minimise steps if you use relative velocity.
Log in to reply
Well, maybe you can post that solution :D I'll like to know how to solve this kind of question using another method. Because i always do it this way, and yeah it needs a lot of energy :\
Nice solution Clean
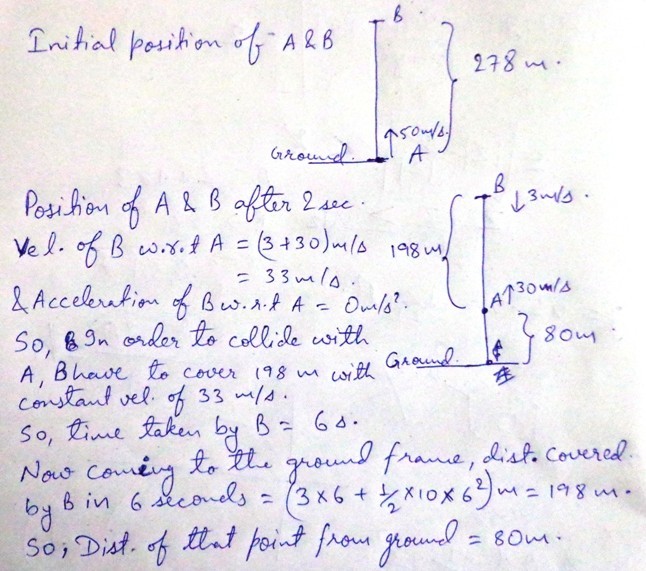 Here is another method to solve.
Here is another method to solve.