Kinematics Problem: Disc/Rod assembly - maximum speed
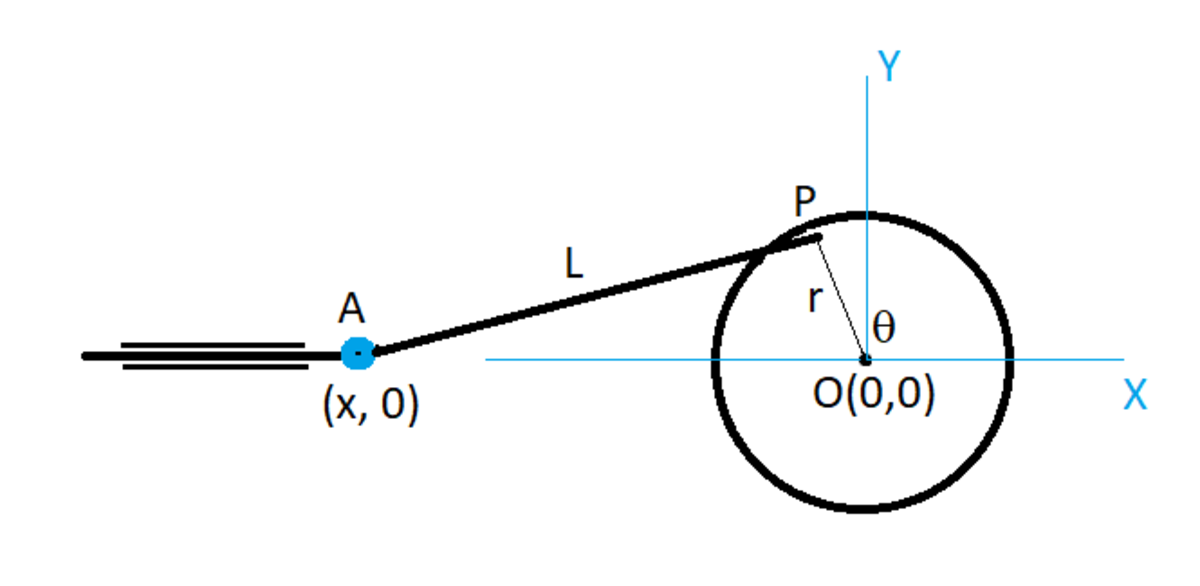
A disc is centered at the origin and is free to rotate about its center. A rod is attached to the disc at point and to another rod that can only move horizontally along the -axis, at point . Both and are revolute joints. If , and the disc rotates at a constant angular velocity of , where is the counter clockwise angle that makes with the positive -axis, find the maximum speed of point , (speed = , and ) , in , where is the -coordinate of point A ( is negative).
Note: The answer is a positive number.
The answer is 13.183.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
O P = R A P = L
Coordinates of P are:
x p = R cos θ y p = R sin θ
Say the link AP makes an angle ϕ with the positive X-axis. Coordinates of point A are then:
x a = − L cos ϕ + R cos θ y a = 0
This gives rise to the constraint equation for the Y coordinate of point P which is:
y p = R sin θ = L sin ϕ
Eliminating ϕ from the equation of x a gives the following equation (Simplification left out):
x a = R cos θ − L 2 − R 2 sin 2 θ
Differentiating wrt. time gives:
v a = ( − R sin θ + L 2 − R 2 sin 2 θ R 2 sin θ cos θ ) ω
The above equation is v a as a function of θ which varies uniformly with time. This is a standard unconstrained maximisation problem which I solved using a script of code. I swept across the range 0 ≤ θ ≤ 2 π and stored the maximum value.
The problem can also be solved by differentiating wrt θ and equating the result to zero, solving, and doing a second derivative test. I have not done so, as programming is convenient here.
The result is:
v a , m a x ≈ 1 3 . 1 8 3