Kinematics Problem : Disc/Rod assembly

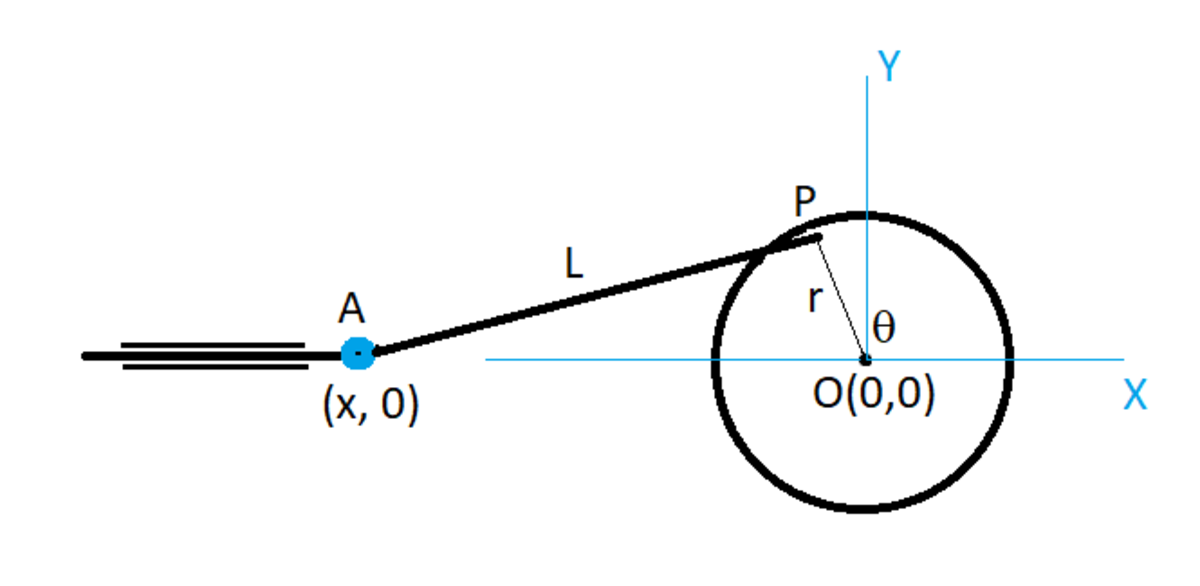
A disc is centered at the origin $O(0,0)$ and is free to rotate about its center. A rod $PA$ is attached to the disc at point $P$ and to another rod that can only move horizontally along the $x$ -axis, at point $A$ . Both $P$ and $A$ are revolute joints. If $\overline{OP} = 50 cm , \overline{PA} = L = 150 cm$ , and the disc rotates at a constant angular velocity of $\omega = \dfrac{d\theta}{dt} = 0.25 rad/sec$ , where $\theta$ is the counter clockwise angle that $OP$ makes with the positive $x$ -axis, find the velocity $v$ of point $A$ , when $\theta = \dfrac{3 \pi}{4}$ , where $v = \dfrac{dx}{dt}$ , in $cm / sec$ , and $x$ is the $x$ -coordinate of point A ( $x$ is negative).

Note: The answer is a negative number.