Kinetic Energy Calculation

Classical Mechanics Level 3

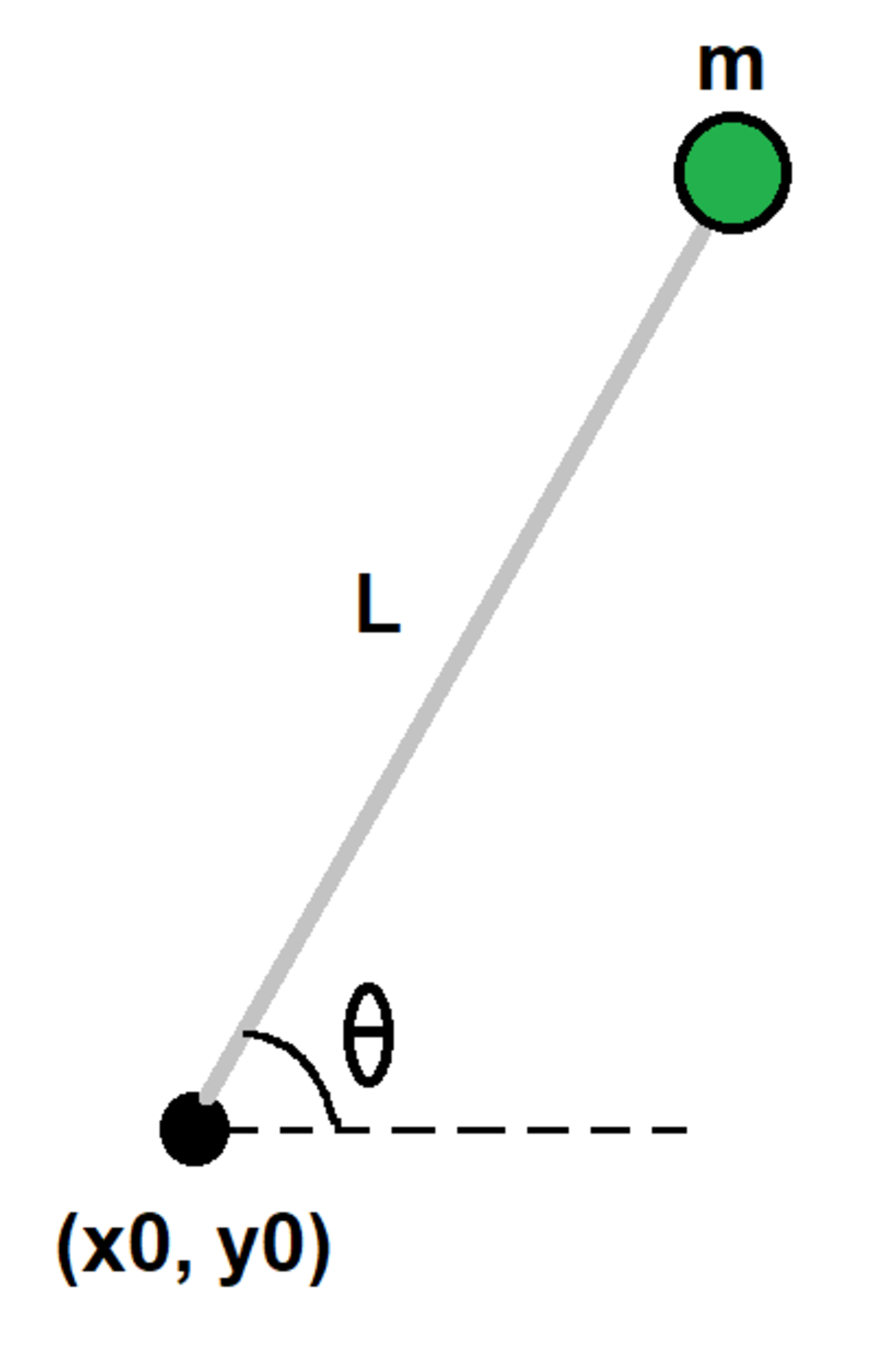
One end of a rod of length L = 1 L = 1 is located at coordinates ( x 0 , y 0 ) (x_0, y_0) . The other end is attached to a particle of mass m = 1 m = 1 . The rod makes an angle θ \theta (in radians) with the horizontal.

At a particular instant, the state of the system is as follows:

x ˙ 0 = 1 y ˙ 0 = 1 θ = π / 3 θ ˙ = − 1 \dot{x}_0 = 1 \\ \dot{y}_0 = 1 \\ \theta = \pi / 3 \\ \dot{\theta} = -1

What is the kinetic energy of the particle?


The answer is 1.866.

Steven Chase by Steven Chase , 37, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Krishna Karthik
Jan 22, 2021

First, we know that x = L cos ⁡ θ x = L\cos{\theta} and y = L sin ⁡ θ y = L\sin{\theta}

With some differentiation with respect to time, x ˙ = − L sin ⁡ θ θ ˙ \dot{x} = -L\sin{\theta} \dot{\theta} and y ˙ = L cos ⁡ θ θ ˙ \dot{y} = L \cos{\theta} \dot{\theta}

But let's not forget the initial conditions. So:

x ˙ = 1 − L sin ⁡ θ θ ˙ \dot{x} = 1 - L\sin{\theta} \dot{\theta}

y ˙ = 1 + L cos ⁡ θ θ ˙ \dot{y} = 1 + L\cos{\theta} \dot{\theta}

Where θ ˙ = − 1 \dot{\theta} = -1 and θ = π 3 \displaystyle \theta = \frac{\pi}{3}

The square of the speed v 2 = 2 + 2 l ( sin ⁡ θ − cos ⁡ θ ) + L 2 v^2 = 2 + 2l(\sin{\theta} - \cos{\theta}) + L^2 ; this is just algebra.

Substituting values, we get E = 2 + 3 2 \displaystyle \boxed{E = \frac{2+\sqrt{3}}{2}}

1 Helpful 1 Interesting 1 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...