Kinetic energy of a hemisphere

Classical Mechanics Level 2

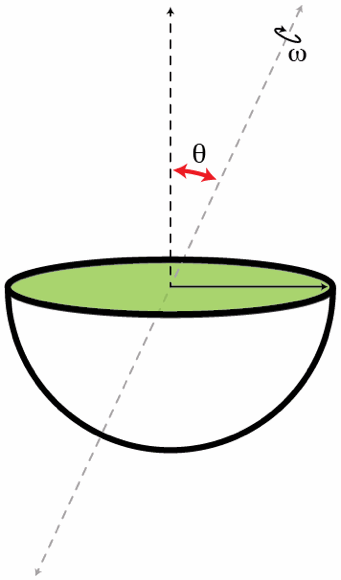
A solid hemisphere of radius R = 0.5 m R=0.5~\mbox{m} and mass M = 1 kg M=1~\mbox{kg} rotates with angular speed ω = 10 rad/s \omega=10~\text{rad/s} about an axis passing through its center O and making and angle θ = 6 0 ∘ \theta=60^{\circ} with the vertical (see the figure below). Determine the kinetic energy in Joules of the hemisphere.


The answer is 5.

View wiki
David Mattingly by David Mattingly

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Consider , if there were two such hemisphere making a sphere of mass 2 M 2M . Both hemispheres would have the same moment of inertia I I . We will derive that I I is independent of θ \theta

Hence, 2 I = 2 5 2 M R 2 ⇒ I = 2 M R 2 5 2I = \frac{2}{5}2MR^2 \Rightarrow I = \frac{2MR^2}{5}

K . E . = 1 2 I w 2 = M R 2 5 w 2 = 5 K.E. = \frac{1}{2}Iw^2 = \frac{MR^2}{5}w^2 = \fbox{5} .

13 Helpful 0 Interesting 1 Brilliant 1 Confused

Can you please explain how M.I. is independent of 'theta' ?

Ahmed Abid Abbash - 7 years, 8 months ago

where did 'theta' go?isn't it related with angular speed?

tasfin mahmud - 7 years, 8 months ago

Why don't you add K = 1 2 I ω 2 + 1 2 m v 2 K=\frac{1}{2}I\omega^2+\frac{1}{2}mv^2 ?

Cody Johnson - 7 years, 8 months ago

Log in to reply

That would have yielded the same answer.

Actually, the MOI i have calculated is not the one that passes through the center of mass.

Actually , K = 1 2 I p w 2 K = \frac{1}{2}I_{p}w^2 can be used directly , if I p I_{p} is about an axis passing through stationary points. Let me show , how to do using

K = 1 2 I c m w 2 + 1 2 M v c m 2 \frac{1}{2}I_{cm}w^2 + \frac{1}{2}M{v_{cm}}^{2} .

Here , v c m = w d v_{cm} = wd , and I c m = I p − m d 2 I_{cm} = I_{p} - md^2 , where d d is the perpendicular distance of c m cm from the axis shown .

Hence, K = 1 2 [ I p − M d 2 ] w 2 + 1 2 M ( w d ) 2 K =\frac{1}{2}[I_{p} - Md^2]w^2 + \frac{1}{2}M({wd})^{2}

= 1 2 I p w 2 \frac{1}{2}I_{p}w^2 .

Here I p I_{p} is used instead of I I , as used in my solution.

kushagraa aggarwal - 7 years, 8 months ago

what is moment of inertia

Kinjal saxena - 7 years, 8 months ago
Lokesh Sharma
Oct 7, 2013

Let the mass of solid hemisphere be M M .

Mass of solid sphere of which this hemisphere is a part = 2 M 2M .

Moment of inertia of whole figure (sphere) = 2 5 × ( 2 M ) R 2 \frac{2}{5} \times (2M)R^{2}

Moment of inertia of half the figure (hemisphere) = 1 2 × 2 5 × ( 2 M ) R 2 \frac{1}{2}\times\frac{2}{5} \times (2M)R^{2} = 2 5 × M R 2 \frac{2}{5} \times MR^{2}

Kinetic energy = 1 2 × I ω 2 \frac{1}{2} \times I\omega^{2} = 5 5

8 Helpful 0 Interesting 0 Brilliant 0 Confused

If you are still not convinced why I I is independent of θ \theta , look at the figure carefully and notice you can take out the left part of the hemisphere and place it on the top of the right part and it would form a complete a hemisphere. I I would remain the same as the distance from the rotational axis is still the same before and after we made the transformation in the rotating object.

  • Left and Right part refer to the part of hemisphere lying left and right with respect to the rotational axis.
  • I I means Moment of Inertia.

Lokesh Sharma - 7 years, 8 months ago

Log in to reply

well, that was a brilliant solution , thanks

niranjan hegde - 7 years, 8 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...