King And Knight
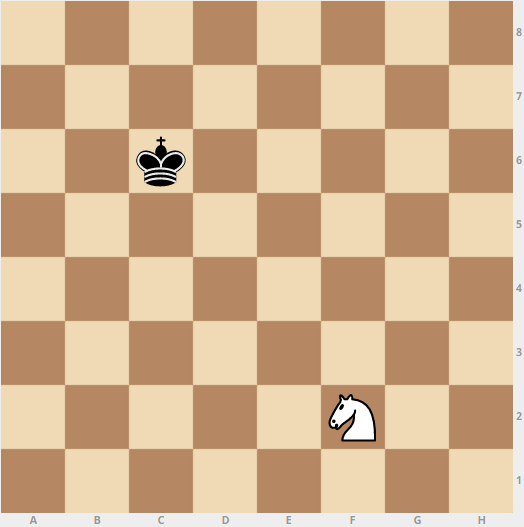
Dimitri places a Black King and a White Knight on 2 distinct squares in an empty chessboard. If the probability that Dimitri places the King and the Knight on the chessboard such that the King is not in check (that is, the Knight is not attacking the Black King), can be expressed as , where and are coprime positive integers, find .
As an explicit example, if the Knight is on , the , , , , and squares are under attack.
This problem is the second of the set Look after the King! .
The answer is 23.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
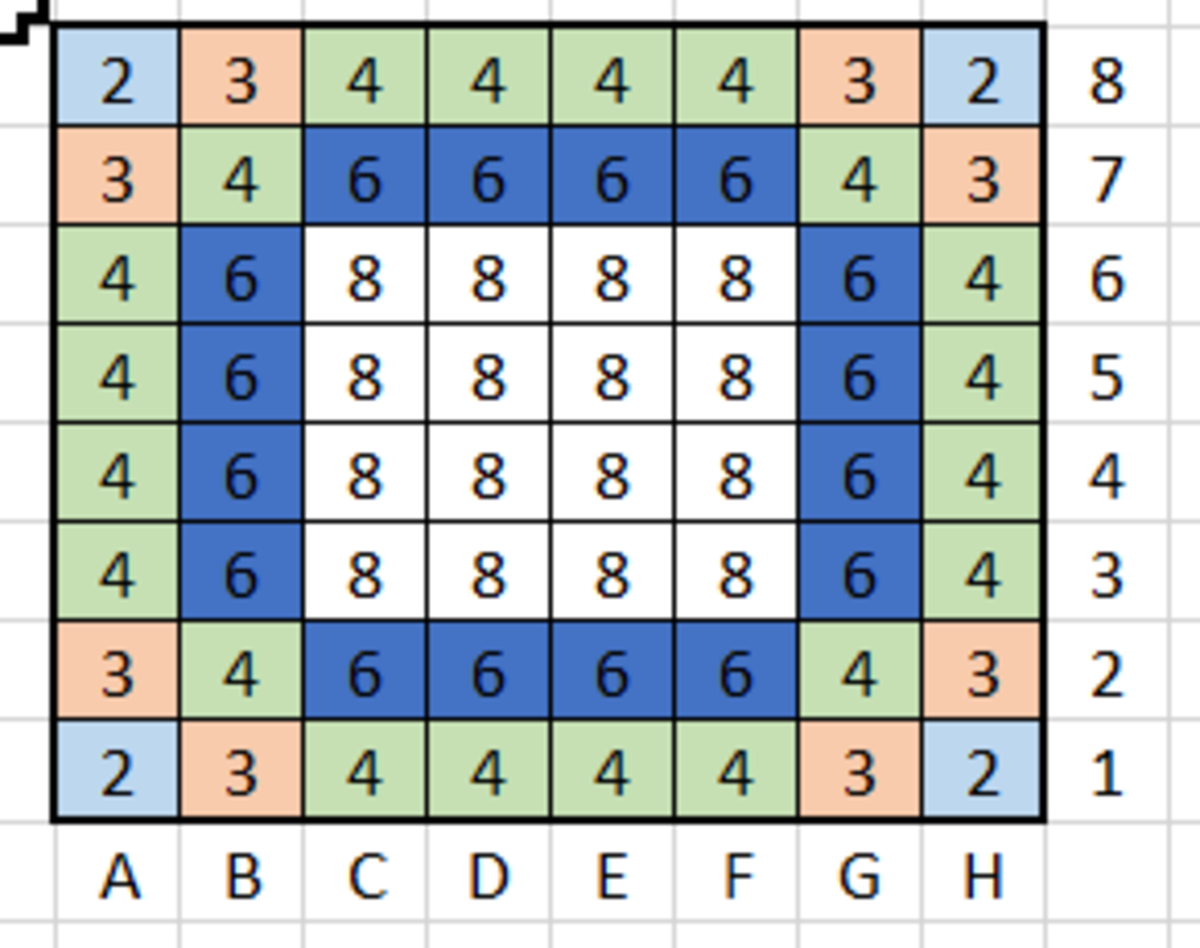
Firstly, note that Dimitri can place the Knight in anyone of the 6 4 squares. As the King and the Knight can't be placed in the same square, Dimitri has 6 3 possible squares to place the Black King. Therefore, there are a total of 6 4 ⋅ 6 3 possible positions.
Secondly, let's divide the possible Knight position in cases:
Consider the square perimeter formed by B and G columns, and 2 and 7 rows. The Knight can be placed on a corner of this square, or on an edge.
In the former case, it will be attacking 4 squares; hence, the King can be placed on the remaining 5 9 squares. As a square has 4 corners, the possibilities are 4 ⋅ 5 9 .
Finally, if the Knight is placed on another square (on the expanded center), it will be attacking 8 squares; so, the King can be placed on the other 5 5 squares. As the expanded center consists of 1 6 squares, the total possibilities are 1 6 ⋅ 5 5 .
Adding up the results and dividing by the total possible positions, the probability is
6 3 ⋅ 6 4 6 1 ⋅ 4 + 6 0 ⋅ 8 + 1 6 ⋅ 5 9 + 1 6 ⋅ 5 7 + 4 ⋅ 5 9 + 1 6 ⋅ 5 5 = 1 2 1 1
Therefore, m + n = 2 3