Kite Problem!
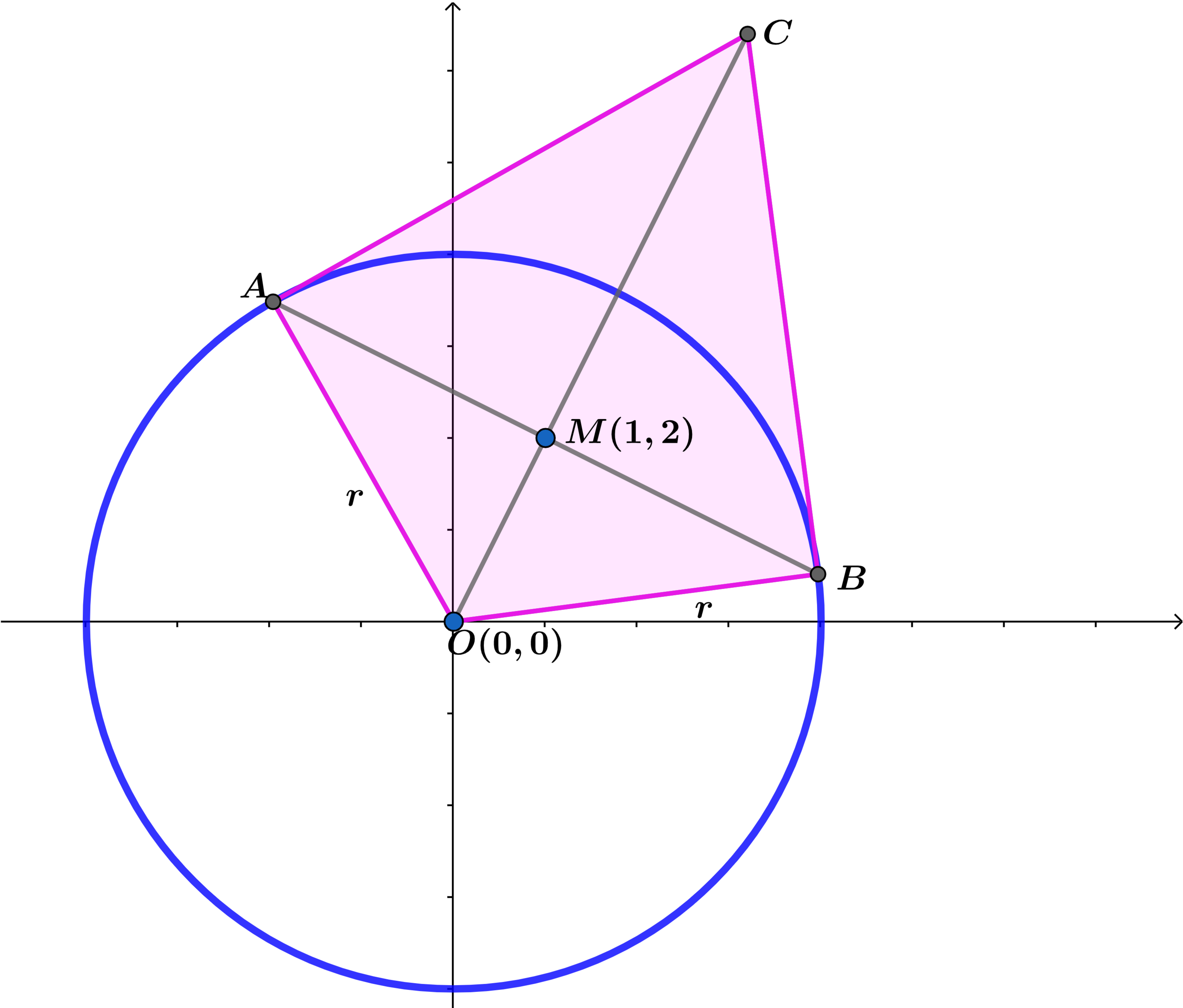
A B is a chord of the circle x 2 + y 2 = r 2 and the tangents at A and B meet at C . If M ( 1 , 2 ) is the midpoint of A B and the area A O A C B = 5 1 1 r 2 , find the radius r of the circle.
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
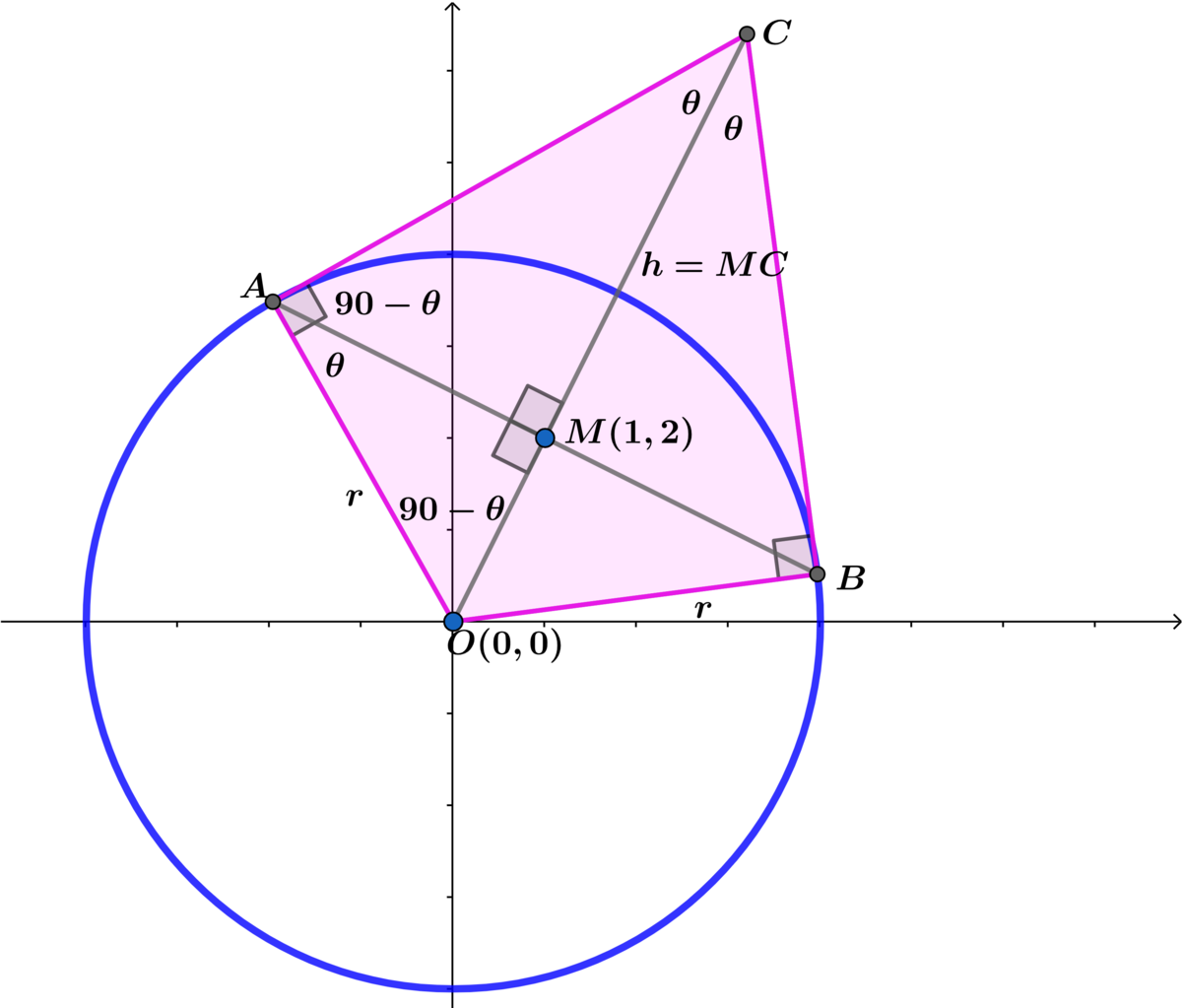
O M = 5 ⟹ M B = M A = r 2 − 5 ⟹ A B = 2 r 2 − 5 ⟹
A △ O A B = 2 1 ( A B ) ( O M ) = 5 r 2 − 5
△ O A M ∼ △ M A C ⟹ 5 r 2 − 5 = r 2 − 5 h ⟹ h = 5 r 2 − 5 ⟹
A △ A C B = 2 1 ( A B ) ( h ) = ( r 2 − 5 ) 5 r 2 − 5
⟹ A O A C B = A △ O A B + A △ A C B = 5 r 2 − 5 r 2 = 5 1 1 r 2
⟹ 5 r 2 − 5 = 5 1 1 ⟹ r = 4
Good to see you :)
The equation of the line
O
M
is
y
=
2
x
. Hence,
y
C
=
2
x
C
.
M
is the midpoint of
A
B
, thus
O
M
⊥
A
B
, so the gradient of the line
A
B
is
−
2
1
and its equation is
y
−
2
=
−
2
1
(
x
−
1
)
⇔
y
=
−
2
1
x
+
2
5
(
1
)
.
On the other hand,
A
B
is the
polar
of the point
C
with respect to the circle, therefore its equation can be written as:
x
C
⋅
x
+
y
C
⋅
y
=
r
2
which rearranges to
y
=
−
y
C
x
C
x
+
y
C
r
2
⇔
y
=
−
2
1
x
+
2
x
C
r
2
(
2
)
(
1
)
,
(
2
)
⇒
2
x
C
r
2
=
2
5
⇔
x
C
=
5
r
2
, therefore, the coordinates of the point
C
are
(
5
r
2
,
5
2
r
2
)
.
Hence,
O
C
=
x
C
2
+
y
C
2
=
5
r
2
and
A
C
=
5
r
4
−
r
2
=
5
r
4
−
r
2
.
This gives A O A C B = 2 A O A C = 2 ⋅ 2 1 ⋅ O A ⋅ A C = r 5 r 4 − r 2 .
Finally, A O A C B = 5 1 1 r ⇔ r 5 r 4 − r 2 = 5 1 1 r ⇔ r 2 ( 5 r 4 − r 2 ) = 5 1 1 r 2 ⇔ r = 4 .
Let O B and O A make angles α and β with the x -axis. Then slope of A B is
cos α − cos β sin α − sin β = − cot ( 2 α + β )
Slope of O C is 2 . Since A B is perpendicular to O C , therefore
tan ( 2 α + β ) = 2 ⟹ cos ( 2 α + β ) = 5 1
∣ A C ∣ = r tan ( 2 β − α )
Areas of triangles △ O A C and △ O B C are equal. So, area of O A C B is
2 × 2 1 × r × r tan ( 2 β − α ) = r 2 tan ( 2 β − α )
= 5 1 1 r 2
⟹ tan ( 2 β − α ) = 5 1 1
⟹ cos ( 2 β − α ) = 4 5
Also, we have
2 r cos α + r cos β = 1
⟹ r = cos α + cos β 2
= cos ( 2 α + β ) cos ( 2 β − α ) 1
= 5 1 × 4 5 1 = 4 .
Rotation about the origin will preserve the distance
∣
O
M
∣
↦
∣
O
M
′
∣
. We then imagine the kite rotated around such that
C
is above the origin, as shown.
https://www.desmos.com/calculator/hysbdxaoc9
∣ O M ′ ∣ = 2 2 + 1 2 ⟹ M ′ = ( 0 , 5 ) . Since O A ′ and O B ′ are radii, then A ′ = ( − r 2 − 5 , 5 ) and B ′ = ( r 2 − 5 , 5 ) .
The gradient of O A ′ = − r 2 − 5 5 , so the gradient of A ′ C ′ = 5 r 2 − 5 ∵ the product of perpendicular gradients = − 1 .
The line A ′ C ′ is described by: y − 5 At C ′ , x = 0 ⟹ y ∴ C ′ = 5 r 2 − 5 ( x + r 2 − 5 ) = 5 r 2 − 5 + 5 = ( 0 , 5 r 2 − 5 + 5 )
The area of a kite is half the product of its diagonals, where ∣ A ′ B ′ ∣ = 2 r 2 − 5 and ∣ O C ′ ∣ = 5 r 2 − 5 + 5 .
We then have that:
Area OACB ⟺ ( 5 r 2 − 5 + 5 ) ( 2 r 2 − 5 ) ⟺ 5 2 ( r 2 − 5 ) 2 3 + 2 ( 5 r 2 − 2 5 ) 2 1 ⟺ 5 2 ( r 2 − 5 ) 2 3 + 5 2 ( 2 5 r 2 − 1 2 5 ) 2 1 ⟺ 2 ( r 2 − 5 ) 2 3 + 2 ( 2 5 r 2 − 1 2 5 ) 2 1 ⟺ ( 2 r 2 − 1 0 ) r 2 − 5 + 1 0 r 2 − 5 ⟺ 2 r 2 r 2 − 5 = 2 5 1 1 r 2 = 2 5 1 1 r 2 = 2 5 1 1 r 2 = 5 2 1 1 r 2 = 2 1 1 r 2 = 2 1 1 r 2 = 2 1 1 r 2
So that r = 0 or r 2 − 5 = 1 1 ⟹ r 2 = 1 6 ⟺ r = ± 4 .
Since we don't get a circle if r = − 4 or r = 0 , the radius r of the circle is 4 .
Let A C = B C = l . We note that ∠ C B O = ∠ C A O = 9 0 ∘ . Then A O A C B = 2 × 2 r l = r l = 5 1 1 r 2 ⟹ l = 5 1 1 r ⟹ r l = 5 1 1 . We also note that △ B M O and △ C B O are similar. Therefore O M B M = r l = 5 1 1 ⟹ B M = 5 1 1 O M = 5 1 1 × ( 1 − 0 ) 2 + ( 2 − 0 ) 2 = 1 1 . By Pythagorean theorem , r 2 = O M 2 + B M 2 = 5 + 1 1 = 1 6 ⟹ r = 4 .