Kite Riddle
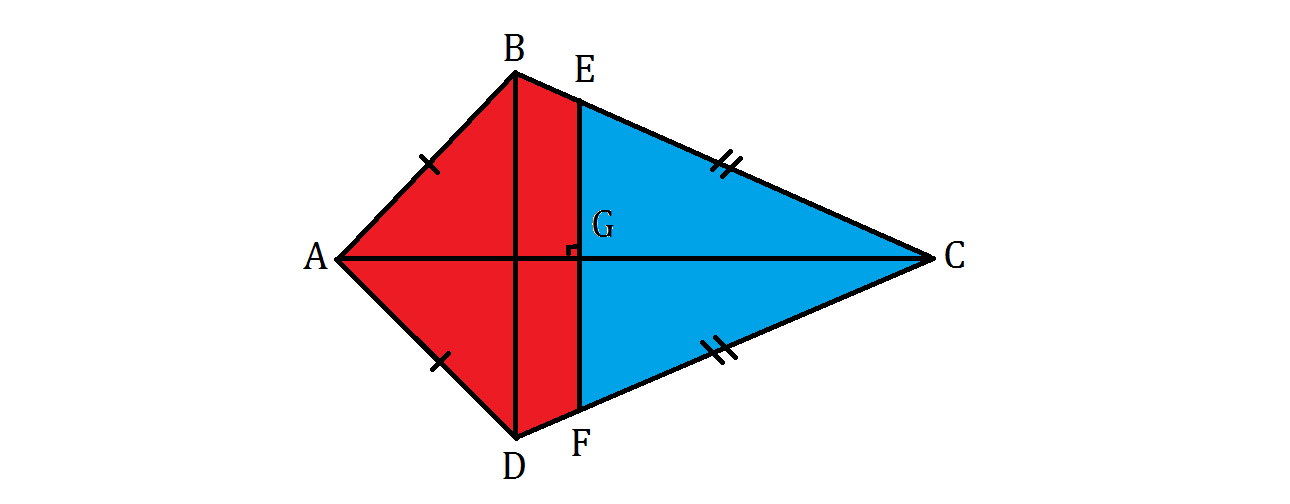
A kite is sectioned into the (red) pentagon and (blue) triangle , where both colored regions have the equal area. The segment is perpendicular to the diagonal with point as its intersection, and the segments , , and are of co-prime integer lengths.
If and , what is the area of the kite ?
The answer is 120.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Since the diagonals of a kite intersect each other at right angles, the point G in this case also acts a midpoint of E F , and G C is a bisector of an isosceles E F C . With E G = a , G C = b , and C E = c for some pairwise co-prime a , b , c , these lengths are, in fact, Pythagorean triples. Then, according to Euclid's formula, we can parametize these lengths, for some co-prime m > n as followed:
a = m 2 − n 2 = ( m + n ) ( m − n )
b = 2 m n
c = m 2 + n 2
We can then calculate the area of the triangle E F C = a b = ( 2 m n ) ( m + n ) ( m − n )
Then we know that 2 B D = 2 b = m n . Thus, the area of the triangle A B C equals to that of E F C because both colored regions have the same area.
Hence, area of A B C = 2 m n ( A C ) = 2 m n ( 8 + b ) = m n ( 4 + m n ) .
Therefore, m n ( 4 + m n ) = 2 ( m n ) ( m + n ) ( m − n )
4 + m n = 2 ( m + n ) ( m − n )
8 + 2 m n = A C = 4 a
b = 4 a − 8
Now if we recreate the figure to be the right triangle A B C such that the colored regions have the same area as shown below, we'll let h be the height A B :
By similar triangle ratios, the maxmum h = b a ( 8 + b ) , and by the area calculation, h = 8 + b 2 a b .
Hence, h 2 = 2 a 2 . h = a 2 .
Now we can set inequality: a 2 > 2 a − 4 > a .
For 2 a − 4 > a , we'll obtain a > 4 .
Then for a 2 > 2 a − 4 , we will obtain 2 − 2 4 ≈ 6 . 8 > a .
Thus, a can only be 5 or 6 , but if a = 6 , then b = 4 × 6 − 8 = 1 6 , which is not pairwise co-prime and not Pythagorean triples.
As a result, a = 5 , and b = 4 × 5 − 8 = 1 2 .
Finally, the area of the kite A B C D = 6 × 2 0 = 1 2 0 .
Note : We can alternatively calculate the length A G = c − a = 1 3 − 5 = 8 .