Knight

Relevant wiki: Chess Puzzles

The fastest way would be to traverse through the diagonal. It can't move directly diagonally, but in two moves it can cover 3 squares. So if we take the bottom left square as #1, and number the squares of the diagonal, the destination cell would be #101. In the first 2 moves it can move to #4, in 4 to #7 and so on. In 2k steps it gets to #(1+k*3), which can reach a maximum of #100, in 66 steps. To move only one step on the diagonal also takes 2 steps (has to be done before getting to #100, since there isn't enough space there to do it). So this method takes 68 steps. It can't be done in 66 steps, since traversing the fastest way through the diagonal only takes us to #100 instead of the required destination, #101; and the 67th step would land on a different colored square, so that's out of the question too (as are all odd answers). So, final answer: 68 . $LaTeX$

Relevant wiki: Chess Puzzles

--Edited version-- Consider the knights moves as shown above.

Move 1: Along the yellow path. 2 steps to the right, 1 step up.

Move 2: Along the muave path. 2 steps to the right, 1 step up.

Move 3: Along the green path (with 1 black square). 2 steps up & 1 step to the right

Move 4: Along the red path (with 2 black squares). 2 steps up & 1 step to the right

This set of 4 moves, leads the knight up 7 squares along the diagonal. That square is marked in the pic as "4 moves". After another such set of 4 moves, the knight is on the 13th square along the diagonal (marked as 8 moves). Hence, after N sets of 4-moves, the knight is at 6 * N+1 square along the diagonal.

For a traversal of 101 squares along the diagonal, the knight would need to perform (101 mod 6) sets = 16 sets. After 16 sets (i.e. 16 * 4 moves = 64 moves ), the knight will be at (6 * 16+1) = 97th square along the diagonal. It has 4 more squares to climb. 4 squares can be climbed in 4 moves as follows:

Move 1: 2 right, 1 up

Move 2: 2 right, 1 up

Move 3: 2 left, 1 up

Move 4: 2 right, 1 up

Hence, 64 + 4 = 68

--Original version--

In 4 moves (2 moves to the right & up + 2 moves up & right), the knight can travel (7 - (setNumber -1)) squares up the diagonal, where setNumber is count of the number of 4-move chunks performed. Hence, at the outset, setNumber = 1 & hence, the knight moves up (7 - (1-1)) = 7 squares. In the next chunk of 4-moves, it moves further by (7 - (2-1)) = 6. Hence, it has moved 13 so far & so on. The total number of squares traversed along the diagonal after any N sets of 4-moves is (7 * setNumber - (setNumber -1)) = 6 * setNumber + 1.

In 101 squares up a diagonal, there are (101 mod 7) = 14, such sections. Hence, after 14, 4-move chunks (i.e. a total of 56 moves), the knight will be at 6 * 14 + 1 = 85. That leaves us with 16 squares to traverse. In 8 more moves it will climb 13 squares (as shown above) leaving it with 3 more squares to climb. In 4 moves one can climb those 3 squares.

Total moves: 56 + 8 + 4 = 68

Relevant wiki: Chess Puzzles

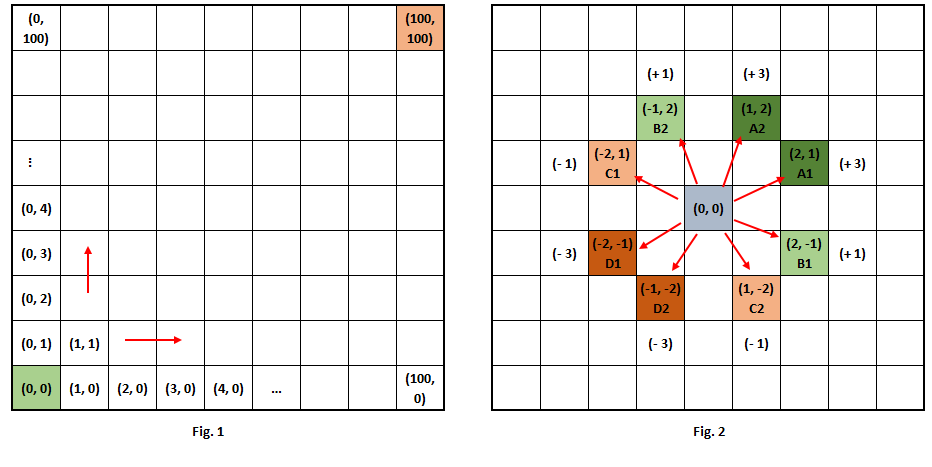
Let's Label the chess board as in Fig. 1. If for every step to the right or upwards we count +1 and for every step to the left or downwards we count -1, we can see that the minimum number of steps we have to take to get to the destiny is the difference between the coordinates of the final position and the initial position and then we add the X and Y coordinates of the resulting vector (Taxicab distance): (100, 100) - (0, 0) = (100, 100) and 100 + 100 = 200.

Now if we label the moves of the chess knight as in Fig. 2 we can see that the effective value of any move is one of four values: +3, +1, -1 or -3. So if we want to get the minimum number of knight-moves to get to the destiny we have to divide the Taxicab distance (200) by the value of the most "efficient" kind of move (+3), this is: 200/3 = 66.666. This implies the minimum value is grater than 66.

Finally if we use the largest amount of A-moves that is 66 we can see that still we need to take 2 additional steps: 200 - 66*3 = 2. The only possible way to do this and get the minimum value is if we add 2 B-moves that have effective value of +1 and we get a minimum number of steps equal to 68.

We can verify that (A2, A1, A2, A1, ... , A2, B1, B2, A1) is one of the possible solutions.

According to the Manhattan metric, the two corners of the board are 200 squares apart, and a single knight move is 3 squares. As such, each move can take the knight at most 3 squares closer to the top right corner. This means that it must take at least $\lceil \frac{200}{3} \rceil = 67$ moves. Since the bottom left and top right squares will always be the same colour, a knight must take an even number of moves to get there, giving a lower bound of 68. And 68 is indeed possible: move with alternating vectors of $(2, 1)$ and $(1, 2)$ , with a single pair of $(-1, 2)$ and $(2, -1)$ inserted somewhere in the middle. (See the diagram in Challenge Master's response to József's solution.)

There are 101 diagonal squares. You start on the first row. Three diagonal squares corrrsponding to three rows are added for every two moves. You reach the 97th (1 + 96) row on the 64th move (2/3 * 96). Four more moves puts you on the 101st diagonal square; 64 + 4 = 68. Note: the 100th diagonal square can be reached on the 66th move, however three more moves are required to advance one diagonal square or 69 moves.

I just took 101 and multiplied it by 2/3, knowing in 2 moves you traverse 3 diagonally, and then rounded it up since you can't finish in a fraction of a square. 101 * 2/3 = 67.333, rounded to 68. Aka, the knight moved 101 squares at 2/3 the rate. I'm sure there's way more to it but idk

Actually I was a bit puzzled because looking at the picture I thought the knight was starting fom the center. Luckily 34 is not a possible answer

Label the diagonal squares as (1, 1), (2, 2), (3, 3), ..., (100, 100), (101, 101). Working backwards from (101, 101) a knight's move will either reduce the row by 2 and the column by 1 OR the row by 1 and the column by 2. For example, from (101, 101) the knight can get to (99, 100) OR (100, 99). From either of those two locations the knight can get back to the diagonal square (98, 98). This strategy is the most efficient way to travel diagonally over the board. The diagonal coordinate reduces by 3 for every 2 moves. Therefore the diagonal coordinate reduces by 96 for 64 moves. In 64 moves the knight efficiently goes from (101, 101) to (5, 5).

Trouble is looming if the knight continues in this manner to (2, 2), so the knight abandons the most efficient strategy for the following four moves that will take it from (5, 5) to (1, 1):

(5, 5) to (3, 4)

(3, 4) to (4, 2) ... backtracking a little to enable synchronization with (1, 1).

(4, 2) to (2, 3)

(2, 3) to (1, 1).

Note that when we add the coordinates of the knights position, the sum changes from odd to even OR even to odd after each move. It will take an even number of moves to get from (5, 5) to (1,1) and this cannot be done in 2 moves. The smallest number of moves is 4, an example of which is shown above.

Therefore the minimum number of moves is 64 + 4 = 68.

It takes the knight 34 moves to move down or across the board to reach the nearest next corner. To reach the diagonally opposite corner requires 68 moves as the knight hs to move across and then down, or down and then across.