Knights of the Round Table
Twelve Knights of the Round Table gathered for a covenant, where the golden goblet filled with blood red wine would be initially put in front of the leader on seat #12, as shown below:
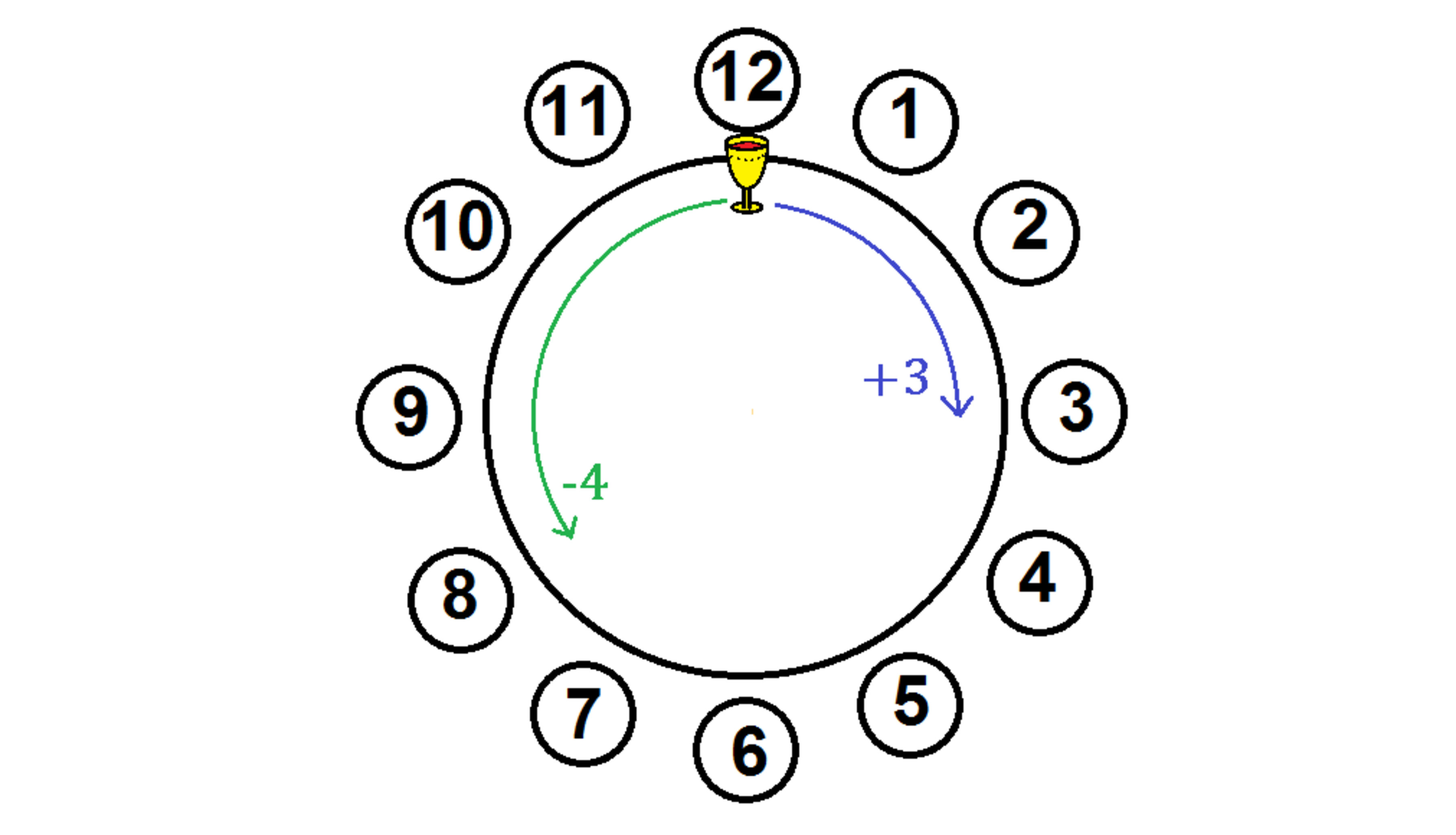
After taking the first sip of wine, the leader then would choose the next drinker, not necessarily the one sitting next to him, by passing the goblet on the turning round table. The table was designed such that each clockwise turn would move the goblet to the next persons and that each counter-clockwise turn to the next persons. As an explicit example, if the leader were to choose the next knight on seat #3 or #8, only one turn would suffice. The table could not be stopped mid-way by others' interference, and the turns must be as minimized as possible for the next knight.
Which knight number would require the most table turns if he were chosen as the second drinker?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
From the question, it is clear that for the first turn, the goblet could land in front of seat #3 or #8. Thereby, we can continue the second turn on either of these seats.
That is, from seat #3, the second turn could lead to 3 + 3 = 6 or 3 − 4 ≡ − 1 ≡ 1 1 ( m o d 1 2 ) , thus stopping at #6 & #11.
Similarly, from seat #8, the second turn could lead to 8 + 3 = 1 1 or 8 − 4 = 4 , thus stopping at #4 & #11.
Continuing on, from seat #4, the third turn could lead to 4 + 3 = 7 or 4 − 4 = 4 , thus stopping at #7 only because we do not want to waste turns on coming back to the origin.
From seat #6, the third turn could lead to 6 + 3 = 9 or 6 − 4 = 2 , thus stopping at #2 & #9.
From seat #11, the third turn could lead to 1 1 + 3 ≡ 1 4 ≡ 2 ( m o d 1 2 ) or 1 1 − 4 = 7 , thus stopping at #2 & #7.
From seat #2, the fourth turn could lead to 2 + 3 = 5 or 2 − 4 ≡ − 2 ≡ 1 0 ( m o d 1 2 ) , thus stopping at #5 & #10.
From seat #7, the fourth turn could lead to 7 + 3 = 1 0 or 7 − 4 = 3 , thus stopping at #10 only, for #3 is already achieved in the first turn.
From seat #9, the third turn could lead to 9 + 3 = 1 2 or 9 − 4 = 5 , thus stopping at #5 only, for we do not want to waste turns on coming back to the origin.
Finally, from seat #5, the fifth turn could lead to 5 + 3 = 8 or 5 − 4 = 1 , thus stopping at #1 only, for #8 is already achieved in the first turn.
From seat #10, the third turn could lead to 1 0 + 3 ≡ 1 3 ≡ 1 ( m o d 1 2 ) or 1 0 − 4 = 6 , thus stopping at #1 only, for #6 is already achieved in the second turn.
As a result, the knight # 1 would require the most turns to bring the goblet in front of him.