Knights on chess
What is the maximum number of chess knights that you can place on a chessboard such that none of them are attacking each other?
Note : The knights in question have no allegiance to white or black. The picture above shows knights which cannot attack each other in one move.
The answer is 32.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
10 solutions
There is a shorter method based on the solution above to prove that 32 is an upper bound. Dissect the chessboard into four parts (upper-left, upper-right, lower-left and lower-right). If there are more than 32 knights on the chessboard, then at least one part of the above must contain at least 9 knights. We just need to number that particular part in order to arrive at a contradiction.
I don't think the first one proves proposition 1.
It shows one particular example of how you could number the squares to show that 32 is achievable, and that under that specific numbering the maximum is 32
A complete proof would have to show that under all possible numbering schemes the maximum would be 32.
Log in to reply
@John H That is incorrect- you only need one numbering scheme to prove the maximum is 32.
Think about it logically- since all squares are paired up, and at most one square in each pair can contain a knight, the maximum is quite obviously going to be 32. Your proof would appear to be a mass over-complication.
Nice solution! You succeeded quite neatly at proving more than 32 knights is impossible, that's a part I struggled with.
wow!!!! what a brain
How is this crazy numbering created??? Is it so obvious that you don't have to explain it? :)) Also, your chessboard is incorrect (or shown on a mirror :)) Also, you shoult start from the top left square because this is the most logical thing to do! :))
Why do you all say "will attack the other in one move" and not just "threatens the other", which is simpler and more direct?
Why are people just trying to sound smart. If you look at the board, it is maxed out. The illustration clearly shows that 32 IS the maximum number of knights that can be placed without being able to vanquish another knight. The wordage used and terminology used does not matter. For everyone trying to downplay this discovery, rethink your perspective.
The method in achieving the answer is trivial. Anyone can extrapolate.
Show us a complete proof then John H.?
The correct number is 48. Remember the rules of the game of Chess. White attacks Black and defends White, Black attacks White and defends Black. The question asked about attacking, NOT about defending. Place White knights in each square of rows 1, 2 & 3 (24 Knights). Place Black knights in each square of rows 6,7 & 8 (24 Knights). White defends (not attacks) White. Black defends (not attacks) Black. And with the gap of open rows 4 & 5, Black and White cannot attack each other. The correct answer is 48.
Skip Meisch [email protected]
Log in to reply
"Note: The knights in question have no allegiance to white or black."
Apologies, on second thoughts I think you can use the first image to construct a proof. It was just the wording didn't make it clear how it was a proof.
I think the following wording would constitute a proof:
Consider the numbered chess board.
-
Any possible arrangement of knights on the board could be converted into a sequence of numbers.
-
To satisfy the requirement that no two knights can threaten each other, then that sequence of numbers could not have any repeated numbers -- Because the repeated numbers on the board always correspond to positions of mutual threat.
-
This means that all viable sequences of numbers would have at most one copy of all the displayed numbers.
-
As the maximum number available is 32, then all arrangements that satisfy the criteria must contain at most 32 knights.
I don't doubt that your solution is valid, but I would suggest the following numbering instead:
12345678
34127856
and similarly for numbers 9 through 32 in the other six rows.
I do not understand Prove 1 . What is the thing you have used there?
Log in to reply
The proof is that there is at most one knight on a square numbered with a 1, and at most one knight on a square numbered with a 2 etc, so by the time you have considered all squares numbers from 1 to 32 there are at most 32 knights and no squares left to consider, so 32 is the maximum.
I say the answer is 48 and I can prove it. [email protected]
It is very easy to notice that a knight always changes it's colour in each move
i.e. WHITE --- BLACK, AND BLACK — WHITE
So, if we place 32 knights in 32 White places , in the next move each will move in Black place. So none can attack each other. If I place one more knight in Black place, then it will be attacked by some white placed knights.
Hence, maximum number of knights is 32.
You mentioned that we cannot extend the 32 knight configuration to a 33 knight configuration because it would be attacked by the white knights. But why must every 33 knight configuration be built on top of the 32 knight configuration that you provided? Couldn't there be a different way to arrive at 33 knights?
Log in to reply
The same thought occurred to me. Yes, if you fill all the white squares you can't place a 33rd knight. But is there an approach which can place (for example) only 29 knights on white squares and then place 4 knights on black squares which can only reach the unoccupied white squares? The answer is no, but it needs to be proved.
Divide the board into four quadrants of 4X4 each. Place a knight onto any square in the bottom row of that quadrant. Doing so immediately eliminates one location in the row immediately above as a place that a knight could be placed. Placing a knight on a second square in the bottom row eliminates another square from the row immediately above. Note that there is no possibility that the first square eliminated can be the same as the second square eliminated. In other words, for each square in the bottom row that gets occupied there is a unique square in the row above that gets eliminated. Also note that the reverse is equally true: for every square in the second row from the bottom that gets occupied there is a unique square in the bottom row that gets eliminated. Generalizing, it is not possible for more than half of the squares in those bottom two rows to be occupied.
This identical logic applies to the top two rows in the quadrant. So no more than half the squares in a quadrant can be occupied, in other words no more than 8 knights in the 4X4 quadrant.
Applying this to all 4 quadrants reveals that the number of knights cannot exceed 32 on the entire board. Note that this does not prove that it is possible for there to be 32 knights. Combining the 4 quadrants might eliminate squares that were otherwise safe when the quadrants were independent. It simply proves that more than 32 occupied squares is impossible.
The other half of the proof is simply to place knights on all 32 squares of identical color. This scenario satisfies the condition of no knight being able to take another. The combination of the proof that more than 32 is impossible and the proof that 32 is possible yields the proof that 32 is the maximum.
The knight's move always moves to an opposite colored square. Therefore, if the knight starts on a black square, it will never be able to land on another black square in a single move, without modification of the rules. To prove this, say we can place more than 32. First, we place 32 on the board, then try to place another - which is impossible, due to the fact that from here there is only one color of square.
A chess board has 64 squares. Each knight you place on the board removes 2 squares, i.e., the square it is on plus the square it can attack. Thus, you can have up to 64/2 = 32 knights which can not attack each other. 🤓
Not rigorous enough. Also a knight attacks more than 1 square
Problem - What if two knights attack the same square? Between the two of them you haven’t shown why they take up more than 3 squares
All knights can't attack same colors as their, so black squares or white squares can either be filled without causing an attack. So the answer is 64/2=32 (which equals to either colors black or white)
Knight attack a square of the opposite colour from the one they occupy.
If the knights are restricted to one colour, by definition they cannot attack one another.
There are 32 squares of each of two colours on a chessboard.
Therefore, 32 knights may occupy those spaces.
But how do you know that 32 is the maximum possible configuration? Why can't it be 33, 34, or more?
If we consider either black or white place diagonally then no knight will hit each other in one move... ( https://ds055uzetaobb.cloudfront.net/image_optimizer/ac4ff75531e35d05c216ce4fc5698b25b74841c7.png ) BECAUSE A KNIGHT PLACED IN A WHITE PLACE IS ONLY ALLOWED TO MOVE TO A BLACK POSITION OR VICE-VERSA!!
But how do you know we can't do better than 32?
Log in to reply
A knight placed in a white place is only allowed to move to a black position or vice versa.... You can see this..!!
And here is another solution
The solution is wrong! the knights can attack each other at the middle of the picture.
All the solutions are wrong! In chess, the word "attack" means to move a piece (or pawn) to a position where it can take an opponent's piece on the next move. While many of the "solutions" given have no knight that can take another knight on the next move, all the knights in all the solutions can attack another knight on the next move.
Like Munem pointed out, this solution does not work. Can you see why?
What David Lawrence says is correct, but I assume the intended question is "What is the maximum number of chess knights that you can place on a chessboard such that none of them can take one another in one move?".
so, as we know 32 is a possible upper bound, and we are trying to prove that it is impossible to squeeze 33 knights into the board.
This is a very rough proof, and you guys can come up with a more accurate and precise one.
Firstly, we need to prove that, the maximum count of knights that can be placed in two adjacent columns is 8.
Proof:
-
if block [Column 1, Row 1-6] has x knights, than each of the knights can attack at least x places in [Column 2, Row 3-8] (move right once and down twice)
-
Hence, in order not to be attacked, there are max 6-x knights in [Column 2, Row 3-8].
-
Next, if there are y knights in [Column 2, Row 1-2], then similarly max 2-y knights in [Column 1, Row 3-4], => max y knights in [Column 2, Row 5-6] => max 2- y knights in [Column 1, Row 7-8]
-
Therefore, the total max count of knights in Column 1 & Column 2 is [Column 1, Row 1-6] +[Column 2, Row 3-8] + [Column 2, Row 1-2] + [Column 1, Row 7-8] = 8
-
So, next, easy peasy.
-
total number of knights should be less than or equal to 8 *4 = 32.
I see that you gave a number of coordinates in your proof. Could you please explain the motivation behind this?
Log in to reply
I was trying to minimise the problem to a smaller sclale, like 2 8, instead of 8 8. While in the scale of 2*8, it intuitively involves some coordinations.
Hmm, i like that you prove that 32 is maximum by only "focusing on 2 adjacent columns at a time".
I think this proof will fail if we have a 10x10 chessboard, right?
Log in to reply
I think, if the column count is even, this solution will always hold.
1. Prove: 32 is maximum.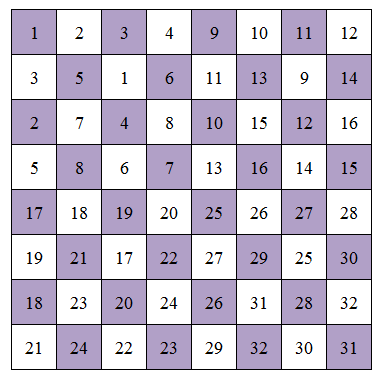
Numbering all squares as above. Notice that if we place 2 knights in 2 squares has the same number, they will attack other in one move.
So, we cannot place more than 32 knights on the chessboard.
2. Prove: 32 can be archived
We can place 32 knights on all white squares in order to none will attack each other as above.