Koch Snowflake - Part 1
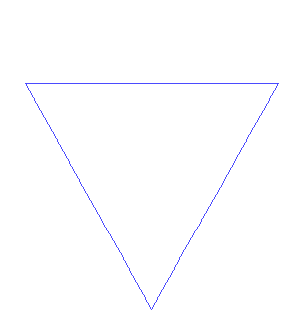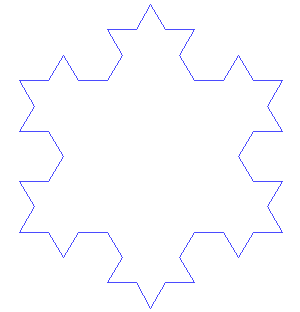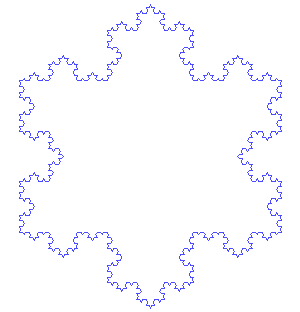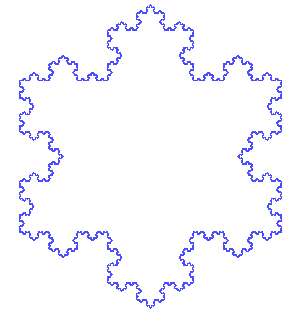 The Koch snowflake is a mathematical curve which starts with a unit equilateral triangle, and then recursively adds an equilateral triangle to the middle third of each line segment. This process continues infinitely. The above is an animation of the first 7 steps.
The Koch snowflake is a mathematical curve which starts with a unit equilateral triangle, and then recursively adds an equilateral triangle to the middle third of each line segment. This process continues infinitely. The above is an animation of the first 7 steps.
Which of the following statements is true of the Koch Snowflake?
Image credit: Wikipedia
If you like Koch Snowflake, you can try Part 2 .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
I did it by instint
I can draw;say,an ellipse such that the koch lies completely in it...so finite area..and since I'm adding triangles ..infinite perimeter.
Log in to reply
If it has a finite area then the shape of the figure remains fixed...so it also must have finite perimeter...
Log in to reply
How does the area being constant imply the shape of the figure it fixed?
I didn't get what you meant by "fixed shape"...can you elaborate?
Awesome
why you have taken side 1 side 2 side 3 different please explain recursive relation
it has finite area and infinite perimeter because as perimeter can enlarge upto many extents
The Snowflake has a finite area because every time it grows , it always encloses a finite area. But as it grows indefinitely its perimeter grows continuously hence has an infinite perimeter.
Call the side length, number of sides, area, and perimeter of the fractal to be l i , n i , a i , p i at time step i , letting l 1 = 1 . Also let a = 4 3 , the area of a single unit triangle, so a 1 = a . Note that p i = l i n i , and trivially n 1 = 3 .
Every time step, the side length is divided by 3 , and the number of sides is multiplied by 4 . Thus l i + 1 = 3 l i and n i + 1 = 4 n i , so p i + 1 = l i + 1 n i + 1 = 3 l i ⋅ 4 n i = 3 4 l i n i = 3 4 p i . Thus p i is a geometric sequence with ratio greater than 1 , and thus it diverges to infinity: it has infinite perimeter .
Recall l i + 1 = 3 l i and n i + 1 = 4 n i . Together with l 1 = 1 , n 1 = 3 , we have l i = 3 i − 1 1 and n i = 3 ⋅ 4 i − 1 .
Also, on time step i to i + 1 , we add n i tiny triangles of side length l i + 1 . Call the area added on time step i to be b i ; thus a i = ∑ j = 1 i b i . Thus b i is:
n i ⋅ 4 l i + 1 2 3
= n i l i + 1 2 a
= 3 ⋅ 4 i − 1 ⋅ ( 3 i 1 ) 2 a
= 3 2 i − 1 4 i − 1 a
= 4 3 a ⋅ ( 9 4 ) i
and so by induction b i + 1 = 9 4 b i for i ≥ 2 . Thus b i is a geometric sequence with ratio between 0 and 1 . As the series b i converges, and a i is just the partial sums b i , we must have a ∞ to be finite, or finite area .
Also, just in case you don't want to get your hands dirty, just head to Wikipedia and get the answer.
For an area, just draw a square surrounded the snowflake and you'll know the truth.
If you put a box around the snowflake, you could enclose the snowflake for all steps. But, there are an infinite number of tiny triangles on the snowflake, making for an infinite perimeter.
But how can enclosing the flake in a box make sure that its area is not changing recursively?
Log in to reply
The area can only get so big. It would always stay inside the box.
isnt it obvious , for any polygon for that instance that recursively progresses will have finite area and infinite perimeter .
Take a square, at each step add 1 to the sides. It recursively progresses and have infinite area and perimeter.
While this a question related to common sense ; still I have a Theoretical Explanation ( by the help of a for loop used in C++ ) :
( 1 ) The Area : In a Triangle,the recursive progress of area :
for( i = 1; i > length ; i++ ) {
Side = side1 + side2 +side3; Recursive = Side/3;
Recursive1 = Recursive - side1; Recursive2 = Recursive - side2; Recursive3 = Recursive - side3;
RFinal = Recursive1 * Recursive2 * Recursive3; RArea = Rfinal*Recursive ;
Area = sqrt(RArea) ;
cout << Area; }
This code will return a finite value.
(ii)Perimeter :
as the perimeter increases infinitely, let l,m,n be the sides of the triangle.
for( i = 1; i > l ; i++) { for( i = 1; i > m ; i++) { for( i = 1; i > n ; i++) { cout<<l + m + n; } } }
This loop will run Infinitely.
Therefore the answer is : a Triangle will have finite area and infinite perimeter for Koch Snowflake curve.