KöMal 04
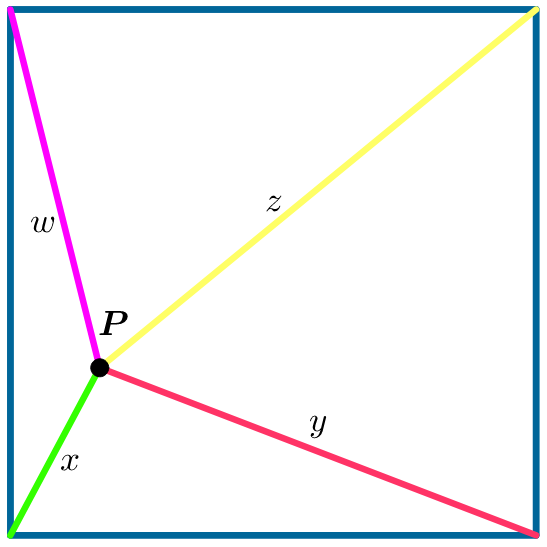
Point
P
is located inside or on the perimeter of a unit square. If the maximum value of its distances from the vertices of the square (
w
+
x
+
y
+
z
) is
a
+
b
, where
a
and
b
are positive integers and
b
is square-free, then find the value of
a
+
b
.
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
- First we observe that the square has symmetrical properties and so we can ignore three quadrants of the square, this leaves us only to analyse the point P lying between 0 ≤ x ≤ 0 . 5 and 0 ≤ y ≤ 0 . 5 .
- If the point P was to leave the square the combined lengths of w,x,y,z would be greater than if P was contained within the square. We can therefore conclude the point P must lie on the edge of the square for the added lengths of w,x,y,z to be a maximum. This case has symmetrical properties too so we can assume it either lies on the y axis of the square or the x axis. For simplification let it lie on the x axis. We are now dealing with points between 0 ≤ x ≤ 0 . 5
- Solving for the total lengths we reach the equation x + ( 1 − x ) + x 2 + 1 + ( 1 − x ) 2 + 1 f o r 0 ≤ x ≤ 0 . 5
- Taking the derivative d x d y ( x + ( 1 − x ) + x 2 + 1 + ( 1 − x ) 2 + 1 ) = x 2 − 2 x + 2 x − 1 + x 2 + 1 x
- Solving for d x d y = 0 we get x = 2 1
- This is a minimum and can be shown by a sign diagram or observing the graph.
- Therefore as x decreases the total length increases.
- As 0 is the lowest value we substitute this into the original equation giving 0 + ( 1 − 0 ) + 0 2 + 1 + ( 1 − 0 ) 2 + 1
- This gives us 2 + 2
- Therefore a + b = 4