Kundabuffer
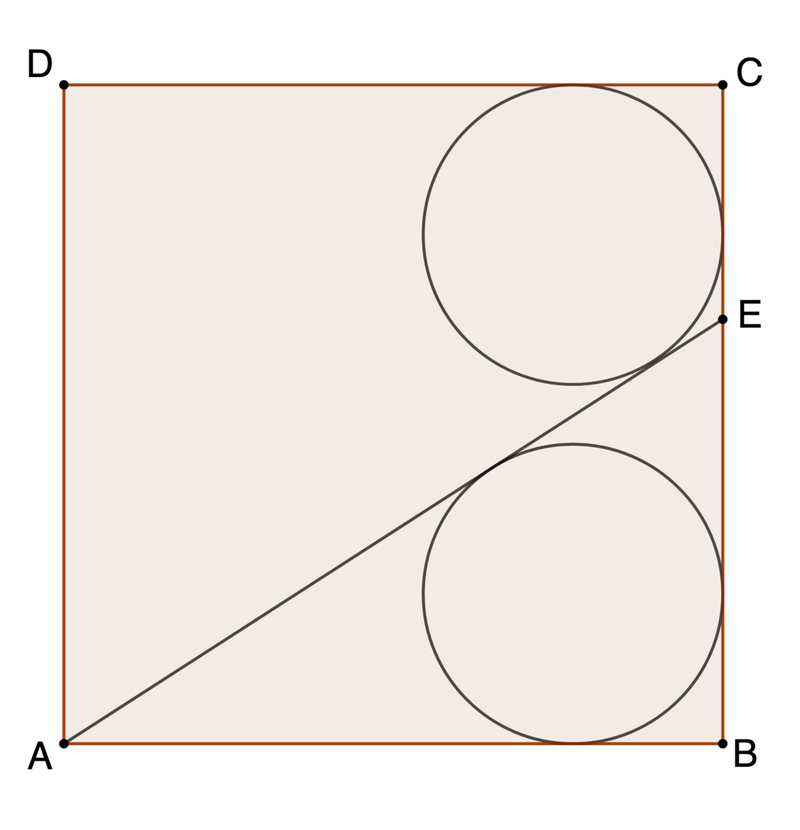
Two congruent circles are inscribed in a unit square A B C D . What is the length of E B ?
Submit ⌊ 1 0 5 ⋅ E B ⌋ .
The answer is 64779.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Much better than mine. +1 +1 +1
Note that you don't need to compute t in the middle of your calculation. Here's what I would have done:
Since we got 1 − t 3 = t + t 2 , then 1 − t 2 = t + t 3 ⟹ E B = cot θ = 2 t 1 − t 2 = 2 t t + t 3 = 2 1 + t 2 .
And because we know that f ( X ) = X 3 + X 2 + X − 1 = 0 has a root t , then f ( X ) = 0 has a root t 2 .
X X + X + X − 1 = 0 ⇒ X ( X + 1 ) = ( 1 − X ) ⇒ X ( X + 1 ) 2 = ( 1 − X ) 2 ⇒ X 3 + X 2 − 3 X − 1 = 0
The rightmost equation above has a root t 2 . By Cardano's method.... can you finish it off?
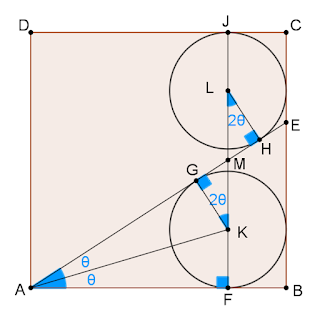 Let
F
,
G
,
H
,
J
be contact points as seen in the figure. Let
K
,
L
be the centers of the circles and
M
the intersection of
A
E
with
J
F
. Denote
∠
K
A
F
by
θ
.
Let
F
,
G
,
H
,
J
be contact points as seen in the figure. Let
K
,
L
be the centers of the circles and
M
the intersection of
A
E
with
J
F
. Denote
∠
K
A
F
by
θ
.
Then,
∠
K
A
G
=
θ
,
∠
G
K
M
=
∠
M
L
H
=
2
θ
.
Hence, we have
J F ⇒ 1 ⇒ cos 2 θ = J L + L M + M K + K F = r + cos 2 θ r + cos 2 θ r + r = 1 − 2 r 2 r ( 1 ) Moreover, on △ K A F ,
tan ( ∠ K A F ) = A F K F ⇒ tan θ = 1 − r r ( 2 ) Furthermore, cos 2 θ = 1 + tan 2 θ 1 − tan 2 θ ( 3 ) .
Combining ( 1 ) , ( 2 ) and ( 3 ) ,
1 − 2 r 2 r = 1 + ( 1 − r r ) 2 1 − ( 1 − r r ) 2 ⇔ … ⇔ 4 r 3 − 8 r 2 + 6 r − 1 = 0 By Cardano's method , this cubic equation gives
r = 6 1 ( 4 − 3 3 3 3 − 1 7 2 + 3 3 3 3 − 1 7 ) ≈ 0 . 2 2 8 1 5 5 4 9 3 6 5 3 9 6 1 Finaly, on △ E A B ,
tan
(
∠
E
A
B
)
=
A
B
E
B
⇒
tan
2
θ
=
1
E
B
⇒
E
B
=
1
−
tan
2
θ
2
tan
θ
⇒
E
B
=
1
−
(
1
−
r
r
)
2
2
1
−
r
r
⇒
E
B
=
1
−
2
r
2
r
(
1
−
r
)
Substituting the value we found previously, we get
E
B
≈
0
.
6
4
7
7
9
8
8
7
1
2
6
1
0
3
9
.
For the answer,
⌊
1
0
5
E
B
⌋
=
6
4
7
7
9
.
Let r denote the radius of the two identical circles. And for simplicities sake, define 0 < h < 1 as the length E B .
The radius of the incircle of a triangle can be expressed as A = r ⋅ s , where A denotes the area of the triangle, and s as the semiperimeter of the triangle.
Let us focus on the bottom right-triangle, its area A is simply 2 h . By Pythagorean theorem , the hypotenuse of this right-triangle is 1 + h 2 , and so its semiperimeter is s = 2 1 ( 1 + h + 1 + h 2 ) . Thus, we can express r in terms of h alone.
A = r s ⇔ r = s A = 1 + h + 1 + h 2 h
Let us rotate the graph picture and plot these points on the Cartesian plane as such:
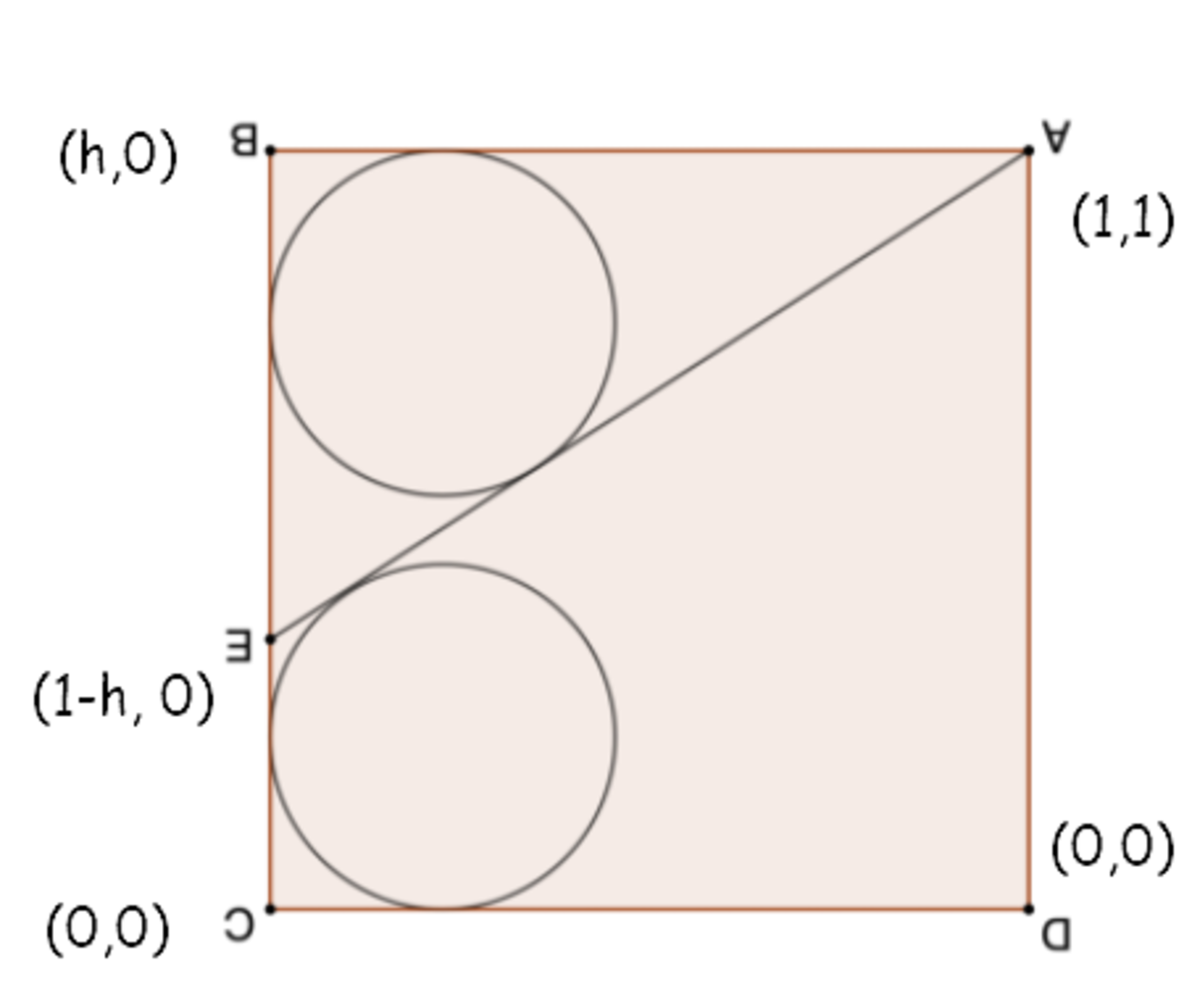
The equation of the straight line E A can be determined as y = h x + ( 1 − h )
And because the bottom left circle (it was previously a top right circle) is tangent to the x -axis, y -axis, and the straight line E A , the equation of this circle of radius r satisfy ( x − r ) 2 + ( y − r ) 2 = r 2 . Substituting y = h x + ( 1 − h ) , we get ( x − r ) 2 + ( h x + 1 − h − r ) 2 = r 2 ⇔ x 2 ( h 2 + 1 ) + x ( − 2 r + 2 h ( 1 − h − r ) ) + ( 1 − h − r ) 2 = 0 .
The above is a quadratic equation whose discriminant (in x ) is 0, ( − 2 r ) 2 − 4 ( h 2 + 1 ) ( 1 − h − r ) ( 2 h + ( 1 − h − r ) ) = 0 . Lastly, we substitute r = 1 + h + 1 + h 2 h , and we can get 2 h 3 − 2 h 2 + 2 h − 1 = 0 . By Cardano's method , E B = h = 3 1 ( 1 − 3 1 3 + 3 3 3 3 2 + 3 4 1 3 + 3 3 3 ) ≈ 0 . 6 4 7 7 9 8 8 . Hence, ⌊ 1 0 5 ⋅ E B ⌋ = 6 4 7 7 9 .
Very nicely done. Did you make use of the discriminant being 0? Had you seen this one before?
Let two circles radii equal to x, CE=b+x and EB=c+x. Write the following relations from figure
b+c+2x=1, on line CB
[(c-b)/2]^2+x^2=[(1/2)-x]^2, on tangent AE between two circles
(1-x+c)^2-(c+x)^2=1, on right triangle AEB
Solve with WolframAlpha, x=0.228155, c=0.419643,
EB=c+x=0.647799
Answer = 64779
Darn I put in the radius instead of EB

Let the radius of the congruent circle be r and ∠ A E B = θ . The the length B C = 1 is given by:
r + r cot 2 θ + r cot ( 9 0 ∘ − 2 θ ) + r r ( 2 + cot 2 θ + tan 2 θ ) ⟹ 2 + t 1 + t = 1 = 1 = r 1 Let t = tan 2 θ
Similarly for A B :
r cot ( 4 5 ∘ − 2 θ ) + r ⟹ 1 − t 1 + t + 1 = 1 = r 1
Therefore.
2 + t 1 + t t t 2 + t + 1 ( 1 − t ) ( t 2 + t + 1 ) 1 − t 3 t 3 + t 2 + t − 1 = 1 − t 1 + t + 1 = 1 − t 1 + t = t + t 2 = t + t 2 = 0
Solving for t using Cardano's method , we get t = tan 2 θ = 3 2 7 1 7 + 2 7 1 1 + 3 2 7 1 7 − 2 7 1 1 − 3 1 ≈ 0 . 5 4 3 6 8 9 0 1 3 . Note that E B = cot θ = 2 t 1 − t 2 ≈ 0 . 6 4 7 7 9 8 8 7 1 ⟹ ⌊ 1 0 5 ⋅ E B ⌋ = 6 4 7 7 9 .