KVPY 2016 geometry
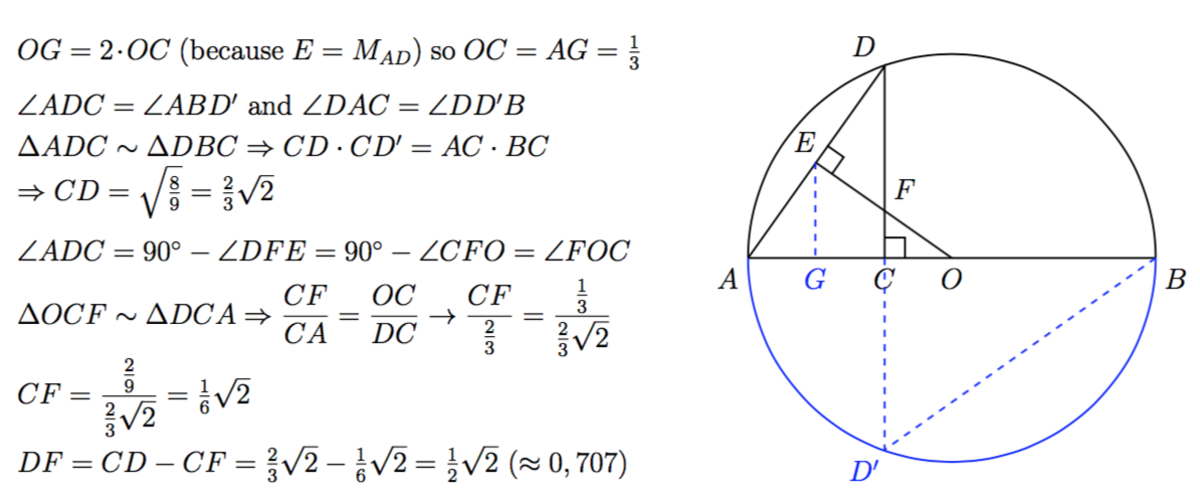
Consider a semicircle of radius 1 unit with diameter A B and center O lies on A B . C is a point on A B such that A C : C O = 2 : 1 . C D is drawn perpendicular to A B with D on the semicircle and O E is drawn perpendicular to chord A D with E on A D .
Let C D intersects O E at H .
Find the numerical value of D H .
Give your answer to 3 decimal places.
The answer is 0.707.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
I wiil use such solution which uses more formulas:
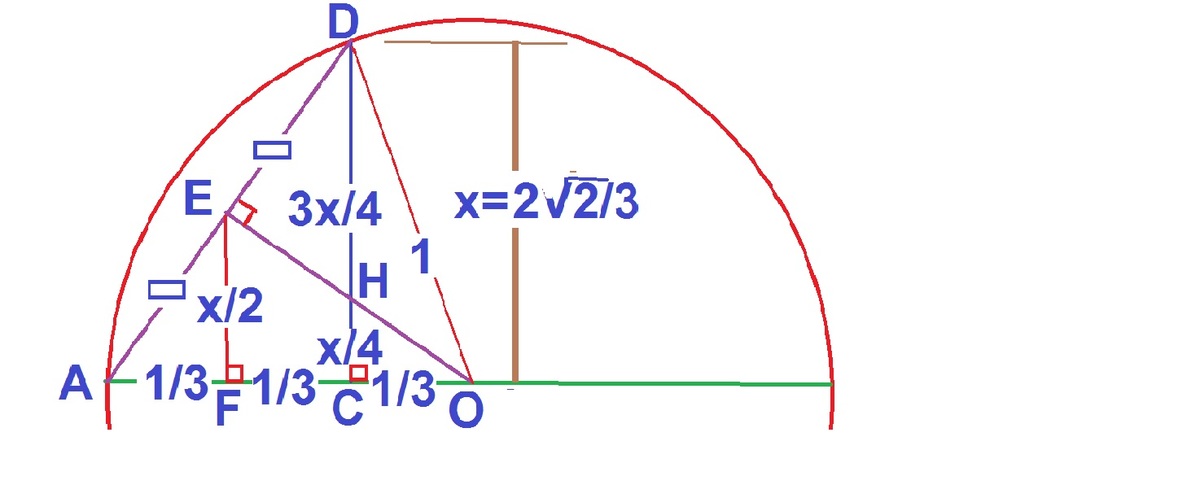
In the figure above, first complete the semicircle to form a circle.
Reflect D in the line A B to get F on the circle. So, let D C = C F = x .
Now by intersecting chord theorem ,
x 2 = ( 3 2 ) ( 3 4 ) hence, D C = 3 2 2 .
Now, Call by θ , the angle A O D and by α , the angle O D E .
In triangle D C O ,
cos θ = 3 1 . And by letting A D = y and applying cosine rule in same triangle, we get
3 1 = 2 1 + 1 − ( A D ) 2 ⇒ A D = 3 2
So that D E = 3 1 .
Now, in triangle D O E ,
cos α = 3 1 . . . ( 1 )
We know that D H = 2 R cos α , where R is circumradius of A O D .
From, R = 4 △ a b c , we get by using ( 1 )
R = 4 △ a b c = 4 × 2 1 × 1 × 1 × 3 2 2 3 2 = 2 6 3 .
So, D H = 2 1 .
I did it exactly the same way in the exam!
hahaha too long
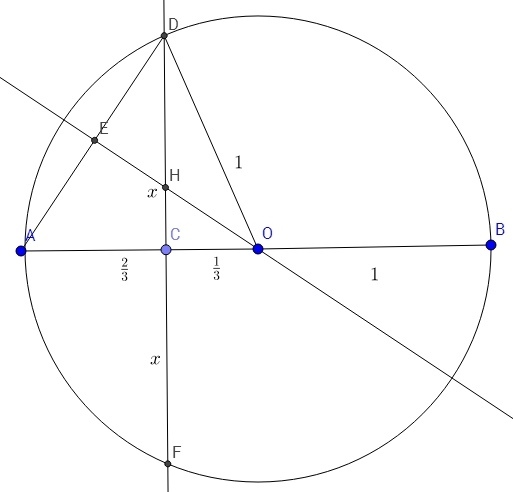
First, drop a perpendicular from E onto A B , intersecting A B at point F . Now, notice that E is the midpoint of A D due to the property that the perpendicular to a chord always bisects it. Since E F is parallel to D C by construction, F is also the midpoint of A H . Additionally E F = 2 1 D C .
Thus A F = F C = C O = 3 1 . This means that C is also the midpoint of F O . By construction again, E F is parallel to H C , hence H C = 2 1 E F .
Therefore, D H = D C − H C = D C − 2 1 E F = D C − 4 1 D C = 4 3 D C . Now, connect D O and observe D O = 1 . Thus by pythagoras' theorem, D C = 1 − 3 1 2 = 9 8 . Finally, we have D H = 4 3 9 8 = 0 . 7 0 7 .
My solution uses 80% trigonometry. I posted this problem to get a pure geometric solution, which you have given perfectly. Thanks for the write-up. Very well written.
Log in to reply
Priyanhsu the big advantage of trigonometry is that it consumes very less time, involves no constructions but only thing u need is to master sine rule and cosine rule. Also, they help solving almost all olympiad problems.
We first get
A
C
=
3
2
,
C
O
=
3
1
and
E
C
=
3
2
2
using
Pythagoras Theorem
on
△
E
C
O
.
We observe that
A
L
=
L
E
since
△
A
O
E
is isosceles and
C
H
=
3
2
2
−
3
E
H
.
We apply
Menelaus Theorem
for
△
E
C
A
with
L
O
as the transversal.
So,
C
O
A
O
×
E
H
C
H
×
A
L
L
E
=
1
[
Actually it should be
−
1
but it doesn't affect the problem as the minus sign is just to indicate that the point
O
does not lie between
A
C
]
.
⇒
3
1
1
×
E
H
C
H
×
A
L
L
E
=
1
.
⇒
E
H
C
H
=
3
1
.
⇒
3
E
H
2
2
−
3
E
H
=
3
1
.
Therefore after solving we get
E
H
=
2
1
.