KVPY 2016 SB Question 5

Geometry Level 4

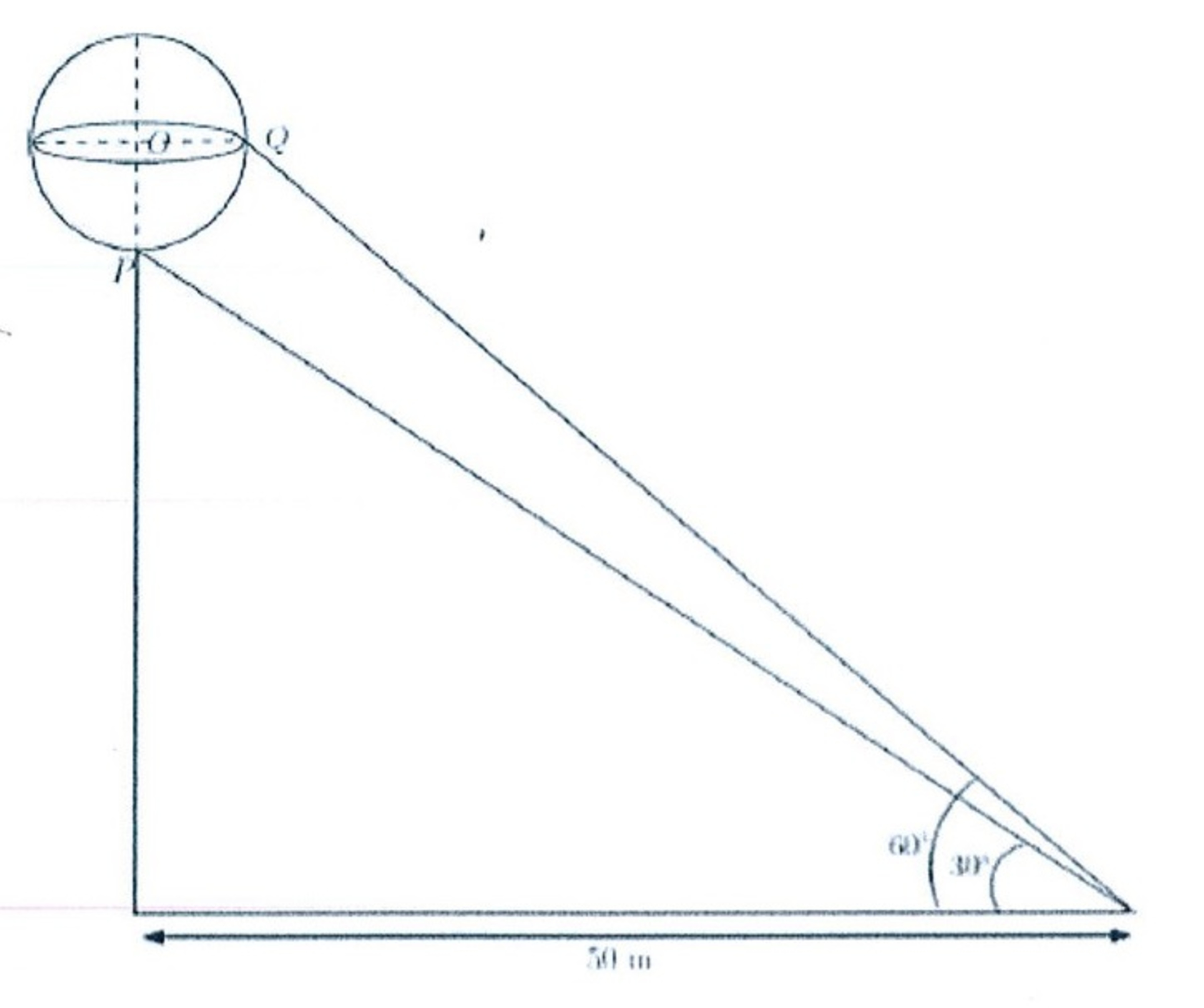
A sphere with centre O O sits atop of a pole as shown in the figure. An observer on the ground is at a distance 50 m from the foot of the pole. The angles of elevation from the observer to the points P P and Q Q are 30 ∘ ^\circ and 60 ∘ ^\circ respectively. Find the radius of the sphere in meter.

Try my set KVPY 2016 SA Questions
100 ( 1 − 1 3 ) 100 \left(1-\frac 1{\sqrt 3} \right) 50 6 3 \frac {50\sqrt 6}3 50 ( 1 − 1 3 ) 50 \left(1-\frac 1{\sqrt 3} \right) 100 6 3 \frac {100\sqrt 6}3

Md Zuhair by Md Zuhair , 20, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Drop a perpendicular from Q Q on A B AB , We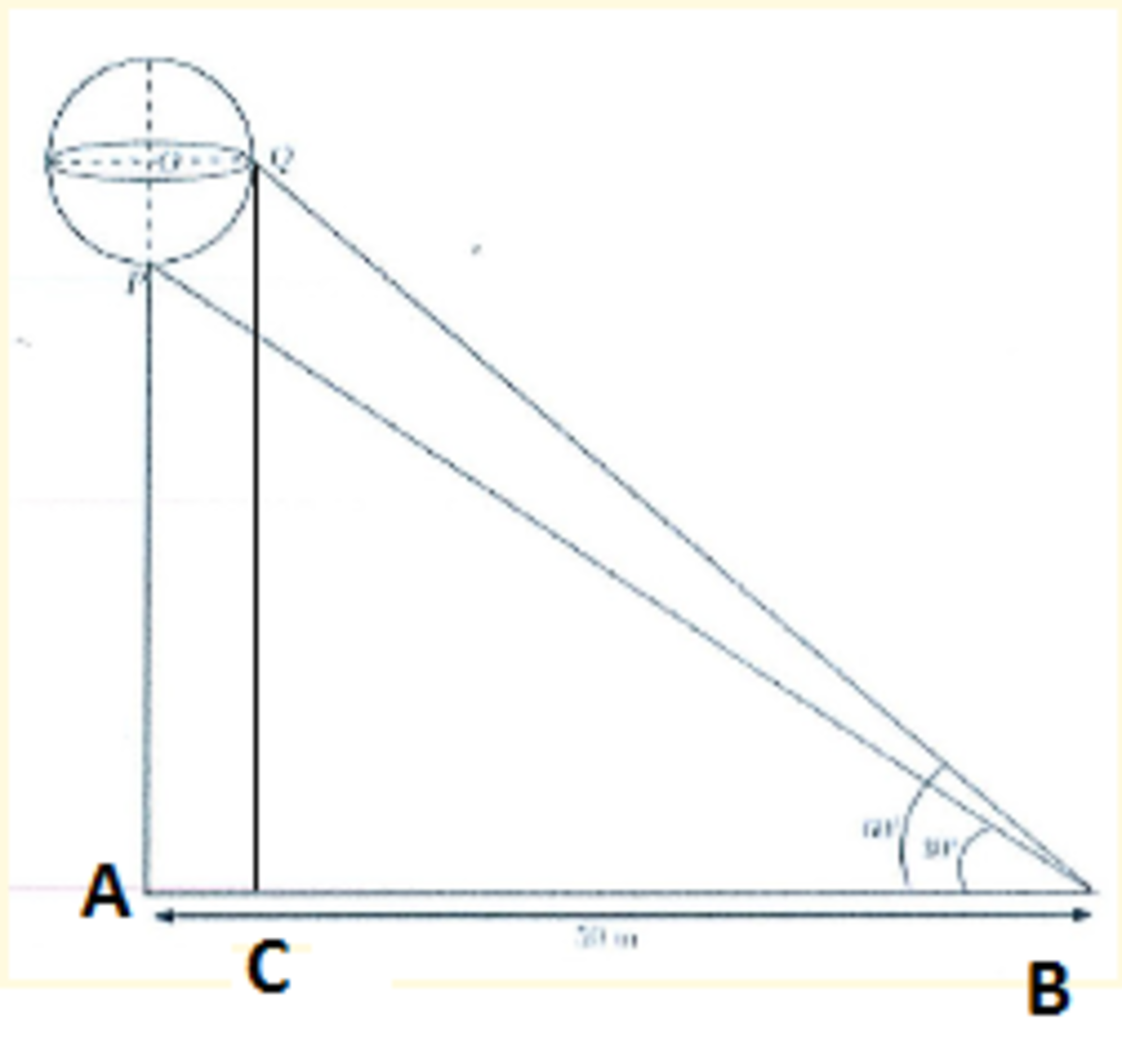 get

Using trigonometry in Triangle A B P ABP , tan ⁡ ( 3 0 ∘ ) = A P 50 , ⋅ ⋅ ⋅ A P = 50 / 3 \tan(30^{\circ})=\frac{AP}{50} ,{\cdot}^{\cdot}\cdot AP=50/\sqrt{3}

Using trigonometry In Triangle Q C B QCB ,` tan ⁡ ( 6 0 ∘ ) = A P + R 50 − R ⋅ ⋅ ⋅ R = 100 3 ( 3 + 1 ) \tan(60^{\circ})=\frac{AP+R}{50-R} {\cdot}^{\cdot}\cdot R=\frac{100}{\sqrt{3}(\sqrt{3}+1)}

And rationalizing the denominator, we get R = 50 ( 3 − 1 ) 3 R=\frac{50(\sqrt{3}-1)}{\sqrt{3}} Which means that answer is C

3 Helpful 0 Interesting 0 Brilliant 0 Confused

Using the Fig. by Mr. Ajinkya Shivashankar, and R as the sphere radius,
P A A B = P A 50 = T a n 30 = 1 3 , ⟹ P A = 50 3 . . . . . . ( 1 ) . \dfrac{PA}{AB}=\dfrac{PA}{50}=Tan30=\dfrac 1 {\sqrt3},~~~~\implies~PA=\dfrac{50}{\sqrt3}......(1). \\ Q C C B = O A A B − A R = P A + R 50 − R = 50 3 + R 50 − R = 3 . ⟹ 50 3 + 50 50 − R = 50 3 ∗ ( 3 + 1 ) 50 − R = 3 + 1. ∴ R = 50 ∗ ( 1 − 1 3 ) . \dfrac{QC}{CB}=\dfrac{OA}{AB-AR}=\dfrac{PA+R}{50-R}=\dfrac{\frac{50}{\sqrt3}+R}{50-R}=\sqrt3.\\ \implies~\dfrac{\frac{50}{\sqrt3}+50}{50-R}=\dfrac{\frac {50}{\sqrt3}*(\sqrt3+1)}{50-R}=\sqrt3 +1.\\ \therefore~R=50*\left (1-\frac 1 {\sqrt3} \right ).

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...